We will discuss below whether Pell's equation is properly named. By this we mean simply: did Pell contribute at all to the study of Pell's equation? There is no doubt that the equation had been studied in depth for hundreds of years before Pell was born. In fact the first contribution by Brahmagupta was made around 1000 years before Pell's time and it is with Brahmagupta's contribution that we begin our historical study.

First let us say what Pell's equation is. We are talking about the indeterminate quadratic equation

nx² + 1 = y²

which we can also write as

y² - nx² = 1

where n is a given integer and we are looking for integer solutions (x, y).

Now, although it is fair to say that Brahmagupta was the first to study this equation, it is equally possible to see that earlier authors had studied problems related to Pell's equation. To mention some briefly: Diophantus examines problems related to Pell's equation and we can reduce Archimedes' "cattle problem" to solving Pell's equation although there is no evidence that Archimedes made this connection.

Let us first note that

(b² - na²)(d² - nc²) = (bd + nac)² - n(bc + ad)²

and

(b² - na²)(d² - nc²) = (bd - nac)² - n(bc - ad)²

From this we see that if

b² - na² = 1 and d² - nc² = 1

then

(bd + nac)² - n(bc + ad)² = 1

and

(bd - nac)² - n(bc - ad)² = 1.

In other words, if (a, b) and (c, d) are solutions to Pell's equation then so are

(bc + ad, bd + nac) and (bc - ad, bd - nac).

This fundamentally important fact generalises easily to give Brahmagupta's lemma, namely that if (a, b) and (c, d) are integer solutions of 'Pell type equations' of the form

na² + k = b² and nc² + k' = d²

then

(bc + ad, bd + nac) and (bc - ad, bd - nac)

are both integer solutions of the 'Pell type equation'

nx² + kk' = y².

The proof that we have given is due to European mathematicians in the 17^th Century (and we shall comment further on it later in this article), but Brahmagupta's lemma was discovered by Brahmagupta in 628 AD. The method was called samasa by the Indian mathematicians but we shall call it the 'method ofcomposition'. In fact this method of composition allowed Brahmagupta to make a number of fundamental discoveries regarding Pell's equation.

One property that he deduced was that if (a, b) satisfies Pell's equation so does (2ab, b² + na²). This follows immediately applying the method of composition to (a, b) and (a, b). Now of course the method of composition can be applied again to (a, b) and (2ab, b²+ na²) to get another solution and Brahmaguptaimmediately saw that from one solution of Pell's equation he could generate many solutions.

This was not the only way that Brahmagupta used the method of composition. He also noted that, using a similar argument to what we have just given, if x = a, y = b is a solution of nx² + k = y² then applying the method of composition to (a, b) and (a, b) gave (2ab, b² + na²) as a solution of nx² + k² = y² and so, dividing through by k², gives

x = 2ab/k, y = (b² + na²)/k

as a solution of Pell's equation nx² + 1 = y².

How does this help? These values of x and y do not look like integers. Well if k = 2 then, since (a, b) is a solution of nx² + k = y² we have na² = b² - 2. Thus

x = 2ab/2 = ab,

y = (b² + na²)/2 = (2b² - 2)/2 = b² - 1

and this is an integer solution to Pell's equation. If k = -2 then essentially the same argument works while if k = 4 or k = -4 then a more complicated method, still based on the method of composition, shows that integer solutions to Pell's equation can be found. So Brahmagupta was able to show that if he could find (a, b) which "nearly" satisfied Pell's equation in the sense that na² + k = b² where k = 1, -1, 2, -2, 4, or -4 then he could find one, and therefore many, integer solutions to Pell's equation. Often he could find trial solutions which worked for one of these values of k and so in many cases he was able to give solutions.

For example, if we attempt to solve 23x² + 1 = y² we see that a = 1, b = 5 satisfies 23a² + 2 = b² so, by the above argument, x = 5, y = 24 satisfies Pell's equation. Applying the method of composition to the pair (5, 24) gives

x = 2×5×24 = 240,  y = 24² + 23×5² = 1151

as another solution. Applying the method of composition again yields

x = 11515,  y = 55224

and yet again gives

x = 552480,  y = 2649601

and so on.

Among the examples Brahmagupta gives himself is a solution of Pell's equation

83x² + 1 = y²

where he notes that the pair (1, 9) satisfies

83×1² - 2 = 9²

and applies his method to find the solution

x = 9,  y = 82.

We can now generate a sequence of solutions (x,y):

(9, 82), 
(1476, 13447), 
(242055, 2205226), 
(39695544, 361643617), 
(6509827161, 59307347962),
(1067571958860, 9726043422151), 
(175075291425879, 1595011813884802)

and so on.

One can only marvel at this brilliant work done by Brahmagupta in 628 AD.

The next step forward was taken by Bhaskara II in 1150. He discovered the cyclic method, called chakravala by the Indians, which was an algorithm to produce a solution to Pell's equation nx² + 1 = y² starting off from any "close" pair (a, b) with na² + k = b². We can assume that a and b are coprime, for otherwise we could divide each by their gcd and get a "closer" solution with smaller k. Clearly a, k are then also coprime.

The method relies on a simple observation, namely that, for any m, (1, m) satisfies the 'Pell type equation'

n.1² + (m² - n) = m².

Bhaskara II now applies the method of composition to the pairs (a, b) and (1, m) to get

n(am + b)² + (m² - n)k = (bm + na)².

Dividing by k we note that

x = (am + b)/k, y = (bm + na)/k

is a solution to

nx² + (m² - n)/k = y².

Since a, k are coprime we can chose m such that am + b is divisible by k. Bhaskara II now knows (but he gives no proof) that when m is chosen so that am + b is divisible by k then m² - n and bm + na are also divisible by k. With such a choice of m he therefore has integer solutions

x = (am + b)/k, y = (bm + na)/k

to the 'Pell type equation' nx² + (m² - n)/k = y² where (m² - n)/k is also an integer.

Next Bhaskara II knows that there are infinitely many m such that am + b is divisible by k. He chooses the one which makes m² - n as small as possible in absolute value. If (m² - n)/k is one of 1, -1, 2, -2, 4, -4 then we can apply Brahmagupta's method to find a solution to Pell's equation nx² + 1 = y². If (m² - n)/kis not one of these values then repeat the process starting this time with the solution x = (am + b)/k, y = (bm + na)/k to the 'Pell type equation' nx² + (m² - n)/k = y² in exactly the same way as we applied the process to na² + k = b². Bhaskara II knows (almost certainly by experience rather than by having a proof) that the process will end after a finite number of steps. This happens when an equation of the form nx² + t = y² is reached where t is one of 1, -1, 2, -2, 4, -4.

Bhaskara II gives examples in Bijaganita and the first we look at is

61x² + 1 = y².

Using the above method he chooses m so the (m + 8)/3 is an integer, making sure that m² - 61 is as small as possible. Taking m = 7 he gets

x = 5,  y = 39

as a solution to the 'Pell type equation' nx² - 4 = y². But this is an equation which Brahmagupta's method solves giving

x = 226153980,  y = 1766319049

as the smallest solution to 61x² + 1 = y².

Why do we suspect that Bhaskara II had no proof of the method? Well there are at least two reasons. Firstly the proof is long and difficult and would appear to be well beyond 12^th Century mathematics. Secondly the algorithm always reaches a solution of Pell's equation after a finite number of steps without stopping when an equation of the type nx² + k = y² where k = -1, 2, -2, 4, or -4 is reached and then applying Brahmagupta's method. If experience of the algorithm is only via examples then, knowing how to proceed when k = -1, 2, -2, 4, or -4 is reached, it is natural to switch to Brahmagupta's method at that point. However, when one writes down a proof it should become clear that the algorithm switching to Brahmagupta's method is never necessary (although can reach the solution more quickly).

The next contribution to Pell's equation was made by Narayana who, in the 14^th Century, wrote a commentary on Bhaskara II's Bijaganita. Narayana gave some new examples of the cyclic method. Here are two of his examples:

103x² + 1 = y².

Choosing a = 1, b = 10 Narayana obtains

103×1² - 3 = 10².

Choose m so that m + 10 is divisible by -3 with m² - 103 as small as possible leads to m = 11 and we obtain

103×7² - 6 = 71².

Next we must choose m so that 7m + 71 is divisible by -6 and m² - 103 as small as possible. Take m = 7 to get the equation

103×20² + 9 = 203².

Continuing, choose m so that 20m+203 is divisible by 9 and m² - 103 as small as possible. Take m = 11 to get the equation

103×47² + 2 = 477².

Now Narayana applies Brahmagupta's method, in the form we gave above for equations with k = 2, to obtain the solutions

x = 22419,  y = 227528.

His next example is a solution of Pell's equation

97x² + 1 = y²

which leads successively, by applying the cyclic method, to the equations

97×1² + 3 = 10²

97×7² + 8 = 69²

97×20² + 9 = 197²

97×53² + 11 = 522²

97×86² - 3 = 847²

97×569² - 1 = 5604²

Finally Narayana applies Brahmagupta's method to this last equation to get the solution

x = 6377352,  y = 62809633

Now the brilliant ideas of Brahmagupta, Bhaskara II and Narayana were completely unknown to the European mathematicians in the 17^th Century. The European interest began in 1657 when Fermat issued a challenge to the mathematicians of Europe and England. Fermat wrote:-

We await these solutions, which, if England or Belgic or Celtic Gaul do not produce, then Narbonese Gaul will.

Narbonese Gaul, of course, was the area around Toulouse where Fermat lived! One of Fermat's challenge problems was the same example of Pell's equation which had been studied by Bhaskara II 500 years earlier, namely to find solutions to

61x² + 1 = y².

Several mathematicians participated in Fermat's challenge, in particular Frenicle de Bessy, Brouncker and Wallis. There followed an exchange of letters between these mathematicians during 1657-58 which Wallis published in Commercium epistolicum in 1658. Brouncker discovered a method of solution which is essentially the same as the method of continued fractions which was later developed rigorously by Lagrange. Frenicle de Bessy tabulated the solutions of Pell's equation for all n up to 150, although this was never published and his efforts have been lost. He challenged Brouncker who was claiming to be able to solve any example of Pell's equation to solve

313x² + 1 = y².

Brouncker found the smallest solutions, using his method, which is

x = 1819380158564160,  y = 32188120829134849

and he sent these to Frenicle de Bessy claiming that they had only taken him "an hour or two" to find.

In Commercium epistolicum Wallis gave two methods of proving Brahmagupta's lemma which are both essentially equivalent to the argument we gave at the beginning of this article based on the result

(b² - na²)(d² - nc²) = (bd + nac)² - n(bc + ad)².

In 1658 Rahn published an algebra book which contained an example of Pell's equation. This book was written with help from Pell and it is the only known connection between Pell and the equation which has been named after him.

Wallis published Treatise on Algebra in 1685 and Chapter 98 of that work is devoted to giving methods to solve Pell's equation based on the exchange of letters he had published in Commercium epistolicum in 1658. However, in his algebra text Wallis put all the methods into a standard form.

We should note that by this time several mathematicians had claimed that Pell's equation nx² + 1 = y² had solutions for any n. Wallis, describing Brouncker's method, had made that claim, as had Fermat when commenting on the solutions proposed to his challenge. In fact Fermat claimed, correctly of course, that for any n Pell's equation had infinitely many solutions.

Euler gave Brahmagupta's lemma and its proof in a similar form to that which we have given above. He was, of course, aware of the work of Brouncker on Pell's equation as presented by Wallis, but he was totally unaware of the contributions of the Indian mathematicians. He gave the basis for the continued fractions approach to solving Pell's equation which was put into a polished form by Lagrange in 1766. The other major contribution of Euler was in naming the equation "Pell's equation" and it is generally believed that he gave it that name because he confused Brouncker and Pell, thinking that the major contributions which Wallis had reported on as due to Brouncker were in fact the work of Pell.

Lagrange published his Additions to Euler's Elements of algebra in 1771 and this contains his rigorous version of Euler's continued fraction approach to Pell's equation. This established rigorously the fact that for every n Pell's equation had infinitely many solutions. The solution depends on the continued fraction expansion of √n. In the continued fraction of the square root of an integer the same denominators recur periodically. Moreover, the pattern in most of the recurring sequence is "palindromic". i.e. up to the last element, the second half of the periodic sequence is the first half in reverse. The last number in the repeating sequence is double the integer part of the square root.

For example √19 has the continued fraction expansion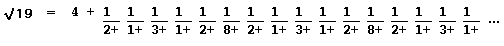 

which recurs with length 6. The convergent immediately before the point from which it repeats is ¹⁷⁰/₃₉ and Lagrange's theory says that

x = 39,  y = 170

will be the smallest solution to Pell's equation

19x² + 1 = y².

To find the infinite series of solutions take the powers of 170 + 39√19. For example

(170 + 39√19)² = 57799 + 13260√19

and

x = 13260, y = 57799

will give a second solution to the equation. Again

(170 + 39√19)³ = 19651490 + 4508361√19

giving

x = 4508361,  y = 19651490

as the next solution. Here are the first few powers of (170 + 39√19), starting with its square, which gives the first few solutions to the equation 19x² + 1 = y²

57799 + 13260√19

19651490 + 4508361√19

6681448801 + 1532829480√19

2271672940850 + 521157514839√19

772362118440199 + 177192022215780√19

262600848596726810 + 60244766395850361√19

89283516160768675201 + 20483043382566906960√19

Although the continued fraction approach to solving Pell's equation is a very nice one for small values on n, the difficulty of the method has been analysed to see if it is the most efficient for large n. A polynomial time method in the length of the input n would be an algorithm which took time bounded by a fixed power of log n (the length of the input). The continued fraction method is not a polynomial time algorithm, and indeed it is now known that no polynomial time algorithm exists for solving Pell's equation

______________________________________________________________________________________________

Books

1. I G Bashmakova and E I Slavutin, History of Diophantine analysis (Russian) : From Diophantus to Fermat "Nauka" (Moscow, 1984).
2. T S Bhanu Murthy, A modern introduction to ancient Indian mathematics (New Delhi, 1992).
3. C Brezinski, History of continued fractions and Padé approximants (Berlin, 1991).
4. L Euler, Elements of algebra : Reprint of the 1840 edition (New York, 1984).
5. C N Srinivasiengar, The history of ancient Indian mathematics (Calcutta, 1967).

Articles

1. A A Antropov, Two methods for the solution of Pell's equation in the work of J Wallis (Russian), Istor. Metodol. Estestv. Nauk No. 32 (1986), 39-49.
2. A A Antropov, Wallis' method of "approximations" as applied to the solution of the equation xغ - nyغ = 1 in integers (Russian), Istor.-Mat. Issled. No. 29 (1985), 177-189, 347.
3. S P Arya, On the Brahmagupta- Bhaskara equation, Math. Ed. 8 (1) (1991), 23-27.
4. C Baltus, Continued fractions and the Pell equations : The work of Euler and Lagrange, Comm. Anal. Theory Contin. Fractions 3 (1994), 4-31.
5. I-Kh I Gerasim, On the genesis of Rédei's theory of the equation xغ -Dyغ = -1 (Russian), Istor.-Mat. Issled. No. 32-33 (1990), 199-211.
6. C Houzel, Introduction a l'histoire de l'analyse diophantienne, in Analyse diophantienne et géométrie algébrique (Paris, 1993), 1-12.
7. K R Johnson, An iterative method for approximating square roots, Math. Mag. 62 (4) (1989), 253-259.
8. G Lachaud, Exactitude et approximation en analyse diophantienne, in L'à-peu-près, Urbino, 1986 (Paris, 1988), 27-45.
9. S Raghavan, The cakravala method, Current Sci. 71 (6) (1996), 490-493.
10. F Schwarz, Wieviele Rinder hat der Sonnengott?, Mitt. Dtsch. Math.-Ver. (2) (1997), 13-18.
11. T N Sinha, Pell's equation: its history and significance, Math. Ed. 5 (1) (1988), 10-15.
12. B L van der Waerden, Pell's equation in the mathematics of the Greeks and Indians (Russian), Uspehi Mat. Nauk 31 (5) (191) (1976), 57-70.