أحد أفضل المعلمين وأفضل المعروفين في ميكانيكا الكم على مدار العشرين سنة الماضية هو ريتشارد فاينمان من معهد كاليفورنيا للتقنية. وقد قدَّم مرجعه المؤلف من ثلاثة أجزاء والمنشور في أوائل ستينيات القرن العشرين «محاضرات فاينمان في الفيزياء»، وهو مرجع قياسي تقارن به المراجع الأخرى للطلاب الجامعيين، وقد ألقى محاضرات عامة في الموضوع نفسه مثل تلك الحلقات في تليفزيون «بي بي سي» عام 1965 التي نشرت تحت عنوان (خاصية القانون الفيزيائي). ولد فاينمان سنة 1918، وكان في قمة عطائه كفيزيائي نظري في الأربعينيات من القرن العشرين؛ حيث كان منهمكا في وضع معادلات نسخة الكم الخاصة بالكهرومغناطيسية، تحت اسم الكهربية الديناميكية للكم، وحصل على جائزة نوبل سنة 1965 عن هذا الإنجاز. ومكانة فاينمان الخاصة في تاريخ نظرية الكم تجعله ممثلا للجيل الأول للفيزيائيين الذين شبُّوا مع كل أسس ميكانيكا الكم وأرسوا كل القواعد الأساسية. وكان على هايزنبرج وديراك أن يعملا في بيئة متغيرة؛ حيث الأفكار الجديدة لا تتوالى بالصورة الصحيحة، ولا العلاقة المنطقية بين مفهوم وآخر - كما في حالة الحركة المغزلية -. تلاحظ بالضرورة على التو، أما جيل فاينمان فقد كانت كل أجزاء اللغز متاحة لهم، ومن الممكن رؤية منطق ترتيبها لأول مرة، وقد لا يكون ذلك في لمحة خاطفة، لكن بالتأكيد بعد قليل من التفكير والجهد الذهني. وهكذا فإن ما يجدر الإشارة إليه أنه في حين كان باولي وأتباعه يفكّرون - والموضوع ما زال ساخنا - أن علاقات عدم اليقين هي المكان المناسب للبدء في مناقشة وتدريس نظرية الكم، توصل فاينمان وهؤلاء المعلمون في العقود الحديثة - الذين ينظرون إلى المنطق بأنفسهم بدلا من إعادة إنتاج أفكار الأجيال السابقة - إلى نقطة بداية مختلفة. قال فاينمان في الصفحة الأولى من مرجعه الخاص بمحاضراته والمخصص لميكانيكا الكم إن العنصر الأساسي في نظرية الكم هو تجربة الشق الطولي المزدوج. لماذا؟ لأن هذه «ظاهرة مستحيلة»، مستحيلة بشكل مطلق لتفسيرها بطريقة كلاسيكية، وبها لب ميكانيكا الكم. وفي الواقع فإنها تتضمن الشيء الوحيد الغامض... والغرائب الرئيسية في كل ميكانيكا الكم.»

ومثل عظماء الفيزيائيين في الثلث الأول من هذا القرن حاولت في كل ما ذكرت سابقا في هذا الكتاب أن أشرح أفكار الكم بمدلول الحياة اليومية. ولنبدأ الآن بالغموض المحوري بأن نزيح الضوء الوامض من خبرتنا اليومية بعيدًا بقدر المستطاع، وأن نشرح العالم الواقعي على ضوء ميكانيكا الكم. ليس هناك شيء في خبرتنا اليومية يمكن أن نحاكيه في عالم الكم، كما أن سلوك عالمِ الكَم ليس له أيُّ شبيه مألوف. ولا يعلم أيُّ إنسان كيف يسلك عالم الكم، وكلُّ ما نعرفه أنه يسلك بتلك الطريقة. وهناك فقط قشتان يمكن التعلُّق بهما الأولى هي أن كلا من الجسيمات (الإلكترونات) والموجات (الفوتونات) تسلك بالطريقة نفسها، فقواعد اللعبة متماسكة. أما القشة الثانية، وكما ذكرها فاينمان فإن هناك شيئًا غامضًا واحدًا فإذا اقتنعت بتجربة الشق الطولي المزدوج يكون أكثر من نصف المعركة قد حُسم؛ حيث إنه وكما يبدو فإن أي موقف آخر في ميكانيكا الكم يمكن شرحه دائمًا بأن نقول: هل تذكر حالة التجربة ذات الثقبين؟ إنه الشيء نفسه. ⁽²⁾

تتم التجربة على النحو الآتي. تخيَّل شاشة من نوع ما – ربما حائط – بها ثقبان صغيران من الممكن أن يكونا شقّين ضيقين كما في تجربة يونج الشهيرة للضوء - لكنهما صغيران - وقد يقوم بالمهمة نفسها ثقبان مستديران صغيران. وعلى أحد جانبي الحائط حائط آخر به كشاف معيَّن. فإذا أجريت التجربة مع الضوء، فمن الممكن أن يكون الكشاف سطحًا أيضًا، يمكن عليه رؤية الضوء والحُزم الداكنة، أو من الممكن أن يكون

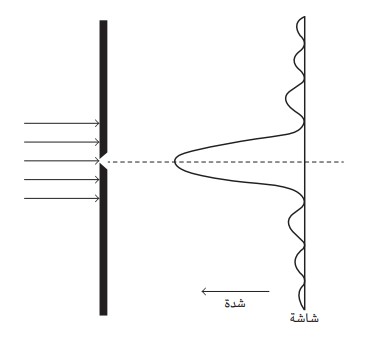
شكل ۸-۱: شعاع إلكتروني يمر خلال شق مفرد طولي ينتج عنه توزيع لأغلب الجسيمات التي تُشاهد في خط مستقيم على امتداد الشق.

الكشاف لوحا فوتوغرافيا، يمكن إظهار الناتج عليه ودراسته فيما بعد. وإذا تم العمل في وجود إلكترونات، فقد تبدو الشاشة مغطاة بترتيب مكون من عدد كبير من كاشفات الإلكترونات، أو من الممكن تصور استخدام كشاف متحرك على عجل يمكن تحريكه كما نشاء لإيجاد عدد الإلكترونات التي تصل إلى بقعة معينة على الشاشة. وليست التفاصيل مهمة ما دامت هناك طريقة ما لرصد ما يحدث على الشاشة. وعلى الجانب الآخر من الحائط المحتوي على الثقبين يوجد مصدر للفوتونات أو الإلكترونات أو أي شيء آخر. وقد يكون هذا المصدر مجرد مصباح أو قاذف إلكترونات مثل ذلك الذي يكون الصورة على شاشة تلفزيونك، ومرة ثانية فإن التفاصيل غير ذات أهمية ما الذي يحدث عند مرور هذه الأشياء خلال الثقبين لتصل إلى الشاشة؛ أي نسق تصنع عندما تصل إلى الكشاف؟ أولا: ابتعد عن عالم الكم للفوتونات والإلكترونات، وانظر إلى ما يحدث في عالمنا اليومي. من السهل رؤية كيف تحيد الموجات عند مرورها خلال الثقوب عند استخدام حوض مليء بالماء ثم غمر النموذج فيه.

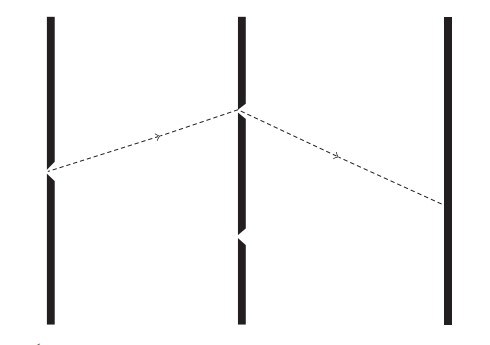
شكل ۸-۲: إلكترون أو فوتون يمر خلال أحد الشقين الطوليين «يجب» تبعا لما هو متوقع أن يسلك بالطريقة نفسها إذا مر خلال شق طولي مفرد.

والمصدر في هذه التجربة مجرد تصميم من نوع ما يهتز إلى أعلى وإلى أسفل ليكون موجات منتظمة. تنتشر الموجات خلال الثقبين مكونةً نسقًا منتظما من القمم والقيعان على طول الكشاف نتيجةً لتداخل الموجات الآتية من كل ثقب. وإذا حجبنا أحدَ الثقبين على الحائط فإن ارتفاع الموجات على الشاشة سيتغير بصورة بسيطة منتظمة، تكون أعلى الموجات هي الأقرب للثقب عبر أقصر مسافة في الحوض، وتقل سعة الموجات على كلٌّ من الجانبين. ويتكون النسق نفسه إذا حجبنا ذلك الثقب وفتحنا الذي كان مغلقًا في السابق. وتتناسب شدة الموجة، التي هي مقياس كمية الطاقة التي تحملها، مع مربع الارتفاع أو السَّعة H²، وتُظهر نسقًا متماثلا لكل ثقب على حدة. ولكن عندما يكون كلُّ من الثقبين مفتوحًا فإن النسق سيصبح أكثر تعقيدًا. وتوجد بالفعل قمة عالية ما بين الثقبين، ولكن الشدة تقلُّ كثيرًا على جانبي القمة؛ حيث إن مجموعتي الموجات يلاشي بعضها بعضًا، ويتكرر تباعًا نسقٌ من ارتفاعات وانخفاضات إذا تحركنا على الشاشة. وقد وجد رياضيا أنه بدلا من أن تكون شدة الثقبين معا هي حاصل جمع كل منهما على حدة (حاصل جمع المربعات) نجد أن الشدة تساوي مربع حاصل جمع سعتهما، وإذا رمزنا لسعة الموجات بـ J و H فإن الشدة I لا تساوي H² + J²

لكنها تصبح:

I = (H+J)²

لتصبح:

I = H² + J² + 2HJ

والحد الإضافي هو المساهمة الراجعة إلى تداخل الموجتين، وإذا سمحنا لقيم J. وH أن تكون سالبة أو موجبة فإن ذلك يفسر بدقة القمم والقيعان لنسق التداخل.

وإذا قمنا بتجربة من نفس النوع مستخدمين جسيمات كبيرة في حياتنا اليومية (تخيل فاينمان بغرابة شديدة تجربةً تتضمن مدفعًا رشاشًا يطلق طلقاته خلال الثقوب الموجودة على الحائط، وقد رُصَّت أجولة مملوءة بالرمل عند الكشاف لالتقاط هذه الطلقات)، ولن نجد أي مدلول للتداخل، وقد نجد بعد إطلاق عدد كبير من الطلقات خلال الثقوب أعدادًا مختلفة من الطلقات في الأجولة المختلفة. وعندما كان ثقب واحد فقط هو المفتوح، فإن نسق انتشار الطلقات حول «الشاشة» ماثل تمامًا لنسق توزيع الشدة لموجات الماء عندما كان ثقب واحد مفتوحًا، ولكن عندما يكون كلا الثقبين مفتوحا فإن نسق توزيع الطلقات في الأجولة يكون بالفعل مساويًا لمجموع التأثير الناتج من الثقبين المنفصلين، ومعظم الطلقات يوجد في المنطقة خلف الثقبين مباشرة، ثم يتلاشى بهدوء دون وجودِ قمم أو قيعان نتيجةً للتداخل. وفي هذه الحالة، وباعتبار أن كل طلقة تمثل وحدة الطاقة، فإن توزيع الشدة يكون:

I = I₁ + I₂

حيث ترمز I₁ ل H² و I₂ل J² في مثال الموجات ولا يوجد مدلول للتداخل.

 وأنت تعلم ما سيأتي بعد ذلك تخيَّل الآن أننا أجرينا التجارب نفسها باستخدام الضوء والإلكترونات. وفي الحقيقة أُجريت تجربة الشق الطولي المزدوج مرات عديدة باستخدام الضوء، ونتج عن ذلك أنساق حيود بالضبط كما في مثال الموجات. لم تُجرَ

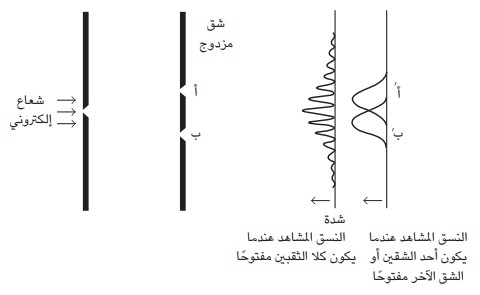
شکل ۸-۳ توضّح التجارب أن النسق المشاهد بالنسبة إلى الإلكترونات والفوتونات، عندما يكون كل من الثقبين مفتوحا فإن هذا النسق لا يماثل حاصل جمع الثقبين عند رؤية كل منهما على حدة.

تجربة الإلكترون بالطريقة نفسها. - هناك مشكلات عند إجراء التجارب بالنسبة إلى الأشياء الصغيرة - لكن أُجريت تجارب مماثلة لتشتت أشعة الإلكترونات عن ذرات موجودة في بلورات. وعليه وللمحافظة على عدم تعقيد الأمور سأتمسك بالتجربة الخيالية للشق الطولي المزدوج مترجمًا ذلك إلى لغة النتائج غير المبهمة التي نحصل عليها من تجارب الإلكترونات الحقيقية. فالإلكترونات مثل الضوء تماما تعطي نسقا للحيود. وماذا بعد؟ أليست هذه مجرد ازدواجية الجسيم / الموجة التي تعلمنا التعايش معها؟ والعبرة هنا أننا اعتدنا التعايش معها لأغراض كتاب طهي الكم، ولكننا لم ننظر بتعمق إلى ما بها من مضامين. وقد حان الوقت لنفعل ذلك فدالة شرودنجر ψ، المتغير في معادلة الموجة الخاصة بها لها علاقة ما بالإلكترون (أو أي جسيم تصفه المعادلة). فإذا كانت موجة، فليس من الغريب أنها تحيد وتنتج نسق تداخل، وإنها لخطوة بسيطة أن نبين أن (ψ) تعمل كسعة الموجة، وأن ²ψ تعمل كالشدة ونسق حيود الإلكترون في تجربة الثقبين هو نسق من ²ψ. وإذا كان في الشعاع إلكترونات عديدة – وهذا تفسير بسيط—فإن ²ψ تمثل احتمالية وجود إلكترون في مكان ما معيَّن.وتندفع آلاف الإلكترونات

شكل 8-4: يبدو أن موجات الاحتمال هي التي تقرر أين يتجه كل «جسيم» في الشعاع وأن موجات الاحتمال تتداخل مثلما تفعل موجات الماء بالضبط.

خلال الثقبين، ويمكن التنبؤ بالمكان الذي تصل إليه على أسس إحصائية مستخدمين هذا التفسير للموجة ψ؛ وهذا هو إسهام بورن العظيم في عملية طهي الكم. لكن ما الذي يحدث لكل إلكترون مفرد؟

 إننا نستطيع أن نفهم بسهولة كافية أن الموجة - قد تكون موجة ماء - تستطيع المرور خلال الثقبين في الحاجز. فالموجة شيء منتشر. لكن الإلكترون ما زال يبدو كجسيم حتى لو صاحبته خصائص تشبه الموجة. ومن الطبيعي أن نعتقد أن كل إلكترون منفرد لا بد وبالتأكيد أن يمر خلال أحد الثقبين ومن الممكن أن نحاول تجريبيا حجب أحد الثقبين كل على حدة دوريًا. وعندما نفعل ذلك فإننا نحصل على النسق المعتاد على الشاشة لتجارب الثقب الأوحد. أما عند فتح الثقبين معًا، فإننا لن نحصل على النسق الناتج من جمع النسقين معًا كما في حالة طلقات الرصاص. وبدلا من ذلك فإننا سنحصل على نسق التداخل كما في حالة الموجات وسنظل نحصل على النسق نفسه حتى لو أبطأنا إطلاق الإلكترونات للدرجة التي يمر فيها إلكترون واحد فقط كل لحظة خلال منظومة الثقبين. ونستطيع أن نخمن أن إلكتروناً واحدًا سيمر من خلال ثقب واحد ويصل إلى الكشاف ليأتي

شكل ٨ ٥: قواعد سلوك الموجة مطلوبة لتحديد ظهور الإلكترون عند أ أو ب، إلا أنه عندما ننظر إلى أ أو ب فنحن إما أن نرى إلكتروناً - جسيمًا – أو لا نرى شيئًا. إننا لا نرى الموجة. ولا نستطيع القول ما الذي يفعله الإلكترون في الحقيقة. أثناء مروره خلال الجهاز

بعده إلكترون آخر وهكذا. فإذا انتظرنا صابرين ليمر عدد كاف من الإلكترونات فإن النسق الذي سيتكون على شاشة الكشاف هو نسق حيود الموجات. ومن المؤكد أنه في حالة الإلكترونات والفوتونات إذا أجرينا ألف تجربة مماثلة في ألف معمل مختلف وجعلنا جسيمًا واحدًا يعبر في كل تجربة، فسنجمع ألف نتيجة مختلفة، لكن بها كلها نسق يتماشى مع الحيود تمامًا كما لو كنا قد جعلنا ألف إلكترون يعبرون معا في واحدة من هذه التجارب ويخضع الإلكترون المنفرد أو الفوتون المنفرد لقوانين الإحصاء عند عبوره من خلال أحدِ الثقبين على الحائط; تلك القوانين التي لا تكون مناسبة إلا إذا «عُرف أولا أن الثقب الآخر مفتوح. وهذا هو الغموض المحوري في دنيا الكم.

نستطيع محاولة الخداع، وذلك بغلق أو فتح أحد الثقبين بسرعة في حين يكون الإلكترون في حالة انتقال خلال الجهاز. ولن يفيد ذلك؛ فالنسق على الشاشة دائما هو «الصحيح» لحالة الثقوب عند لحظة مرور الإلكترون من خلالها. ويمكن أن نختلس النظر لنرى من أي الثقبين يمرر الإلكترون. وعند إجراء تجربة مماثلة لهذه التجربة تأتي النتيجة أكثر غرابة. لنتخيل تصميمًا يسمح لنا بتسجيل أيُّ الثقبين يعبر الإلكترون من خلاله، ويتركه ليعبر ويصل إلى شاشة الكشاف. وهنا تسلك الإلكترونات مسلكًا عاديا كأي المشاهد جسيمات في الحياة اليومية تحترم نفسها. ونرى الإلكترون دائمًا عند ثقب أو عند الآخر، وليس عند الثقبين أبدًا في آن واحد والآن فإن النسق الذي يتكون على شاشة الكشاف سيكون مكافئًا تمامًا لنسق الرصاصات دون وجود أي أثر للتداخل. وفي هذه الحالة، لا تعرف الإلكترونات ما إذا كان الثقبان مفتوحين أم لا فحسب، لكنها تعرف إذا كنا نراقبها أم لا، وعليه تُكيّف من سلوكها وفقًا لذلك. ولا يوجد مثال أوضح من ذلك لتداخل مع التجربة. وعندما نحاول النظر إلى موجة الإلكترون المنتشرة نجدها تنهار إلى جسیم محدد، أما إذا كنا لا ننظر فإنها تتحرك هي نفسها بكل الاحتمالات. وبمدلول احتمالات بورن فإن الإلكترون قد أصبح مضطرًا، بناءً على قياساتنا، لاختيار مسار واحد من احتمالات عديدة. فهناك احتمال أكيد أن ينفذ من أحد الثقبين، وهناك احتمال مكافئ أن يتجه إلى الثقب الآخر، وينتج احتمال التداخل هذا نسق الحيود عند الكشاف. ولكن عندما نكتشف الإلكترون، يكون في مكان واحد مما يغير من نسق الاحتمالية في المستقبل - بالنسبة إلى الإلكترون - ومعروف الآن بالتأكيد أي الثقبين يمر منهما. أما إذا لم ينظر أحد إليه، فحتى الطبيعة نفسها لا تعرف من أي الثقبين مر الإلكترون.

هوامش

(2) The Character of Physical Law, page 130.