


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات | النموذج الثنائي لمسائل البرمجة الخطيةDuality in Linear Programming:العلاقة بين النموذج الأول والنموذج الثنائي: |
|
|
|
أقرأ أيضاً
التاريخ: 29-1-2022
التاريخ: 27-1-2022
التاريخ: 30-1-2022
التاريخ: 30-1-2022
|
العلاقة بين النموذج الأول والنموذج الثنائي:
1- ان تحويل النموذج الثنائي إلى نموذج ثنائي يتحول إلى نموذج أول.
2- المصفوفة (m x n) A للنموذج الأول تعطي المصفوفة (n x m) للنموذج الثنائي.
3- لكل قيود النموذج الأولى توجد علاقة لمتغيرات النموذج الثنائي والعكس صحيح.
4- لكل متغير في النموذج الأول، توجد علاقة له بقيود النموذج الثنائي والعكس صحيح.
5- لكل حل ابتدائي للنموذج الأول.
أ- 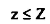
ب- 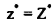
ج- إذا كان  ومنها
ومنها
6- إذا كان النموذج الأول يوجد له حل أمثل فإن النموذج الثنائي له حل أمثل.
7- إذا كان النموذج الأول له حل غير محدود فإن النموذج الثنائي لا يوجد له حل والعكس صحيح.
ويمكن شرح العلاقة بين النموذج الأول (primal pnoblem) والنموذج الثاني (Dual problem) بواسطة العلاقة الرياضية التالية:

وبحل المسألتين كل على حدة بواسطة طريقة السمبلكس تلاحظ الحل في الجداول (6.3) و (6.4).
المعلومات التالية يمكن استنتاجها.
[ الحل الأمثل لمعادلة z للمسألة الأولى ] = [ الفرق ما بين الشمال واليمين لقيود المسألة الثنائية المصاحبة للمتغيرات].
جدول (6.3)
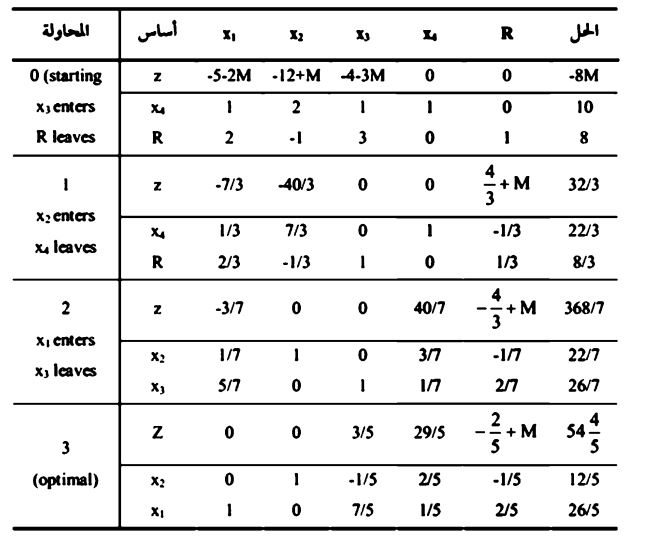

وباقي المعلومات التي يمكن تحديدها في الشكل 6.1.

وهذه النتائج يمكن تعميمها لزوج المسألة الأولى والثنائية.
1- لكل من الحل الابتدائي للمسألة الأولى والثنائية.

2- الحل الأمثل للمسألة الأولي والثنائية
(دالة الهدف لمسألة تعظيم) = (دالة الهدف لمسألة تصغير)



|
|
|
|
هل يمكن أن تكون الطماطم مفتاح الوقاية من السرطان؟
|
|
|
|
|
|
|
اكتشاف عرائس"غريبة" عمرها 2400 عام على قمة هرم بالسلفادور
|
|
|
|
|
|
|
جامعة الكفيل تقيم ندوة علمية عن الاعتماد الأكاديمي في جامعة جابر بن حيّان
|
|
|