
الطيوف الاهتزازية - الدورانية لجزيئات ثنائية الذرة
 المؤلف:
الدكتور محمد انور بطل
المؤلف:
الدكتور محمد انور بطل
 المصدر:
الفيزياء الذرية والجزيئية
المصدر:
الفيزياء الذرية والجزيئية
 الجزء والصفحة:
ص 404
الجزء والصفحة:
ص 404
 17-2-2022
17-2-2022
 2489
2489
الطيوف الاهتزازية - الدورانية لجزيئات ثنائية الذرة
1- الطاقة الإهتزازية الدورانية:
تعطى علاقة الحد الطيفي الاهتزازي والدوراني ب
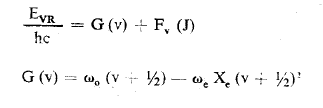
حيث α تعرف تغير ثابت العطالة مع الإهتزاز. عند أخفض سوية اهتزازية (0 = v) نجد:
2 - قواعد الاصطفاء في الإصدار والإمتصاص:
a) — حتى يكون الإنتقال مسموح يجب أن يكون في البداية مسموح بقاعدة الإصطفاء الإهتزازية فمن أجل XY كل الإنتقالات الاهتزازية مسموحة. وممنوعة في حالة X2. من بين الجزئيات ثنائية الذرة فقط الجزيئات ذات الذرات المتشابهه وX2 سيكون لها طيف اهتزازي – دوراني اصداري وامتصاص
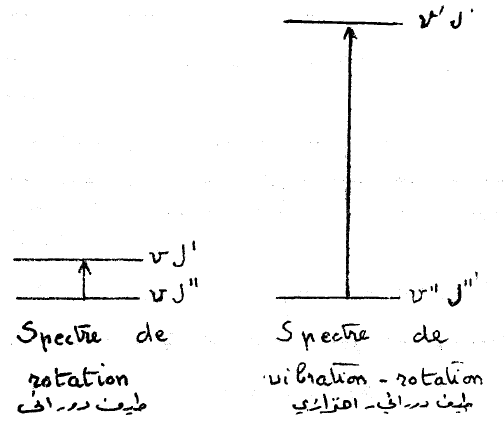
الشكل (1)
b) - في حالة اهتزاز جزئية XY يوجد عزم الإنتقال الإهتزازي حسب oz. وقاعدة الاصطفاء الدورانية نحصل عليها من العلاقة:
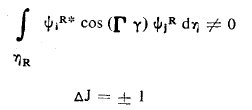
والشكل (1) يعطي مخطط الإنتقال بين سويات الطاقة في هذه الحالة .
3- طيوف الإصدار والامتصاص :
من أجل كل انتقال اهتزازي نحصل على سلسلة خطوط طيفية اهتزازية - دورانية بصورة عامة ندعوها الأفرع. O, P, Q, R, S وهي مميزة ب:
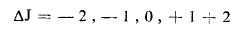
فالسلسلة المعرفة ب 1 + = ΔJ تدعى الفرع R والمعرفة 1 - = ΔJ تدعى الفرع P —الاعداد الموجية التابعة لهذا الفرعان تعطى بالعلاقتين :
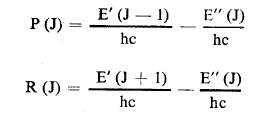
حيث فرضنا أن "J = J. بتعويض في هاتين العلاقتين علاقة الحد الطيفي نجد :

تصبح :
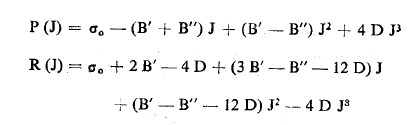
حيث:
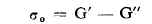
ترمز لمركز قطاع الاهتزاز- الدوران . اذا أهملنا تأثير تشويه الطرد المركزي (0 = D) تصبح المعادلات السابقة بالشكل :

ومن الممكن أن نكتب المعادلتان تحت شكل واحد :
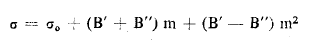 مع:
مع:

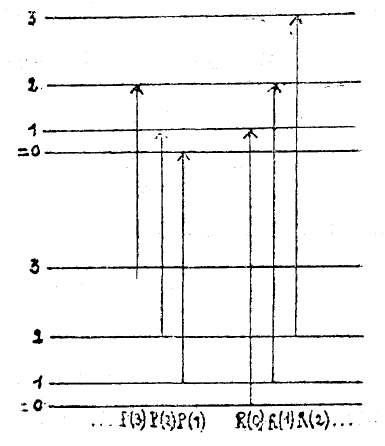
الإنتقالات الاهتزازية - الدورانية (1)R(0), R و (2)P(1), P تعطى على الشكل (1) ومن المهم ملاحظة بأنه لايوجد خط طيفي P(0).
والشكل (2) يبين كيف تتراص الخطوط الطيفية أكثر فأكثر في الفرع R وأن الخطوط الطيفية تتراص أقل فأقل من الفرع P.
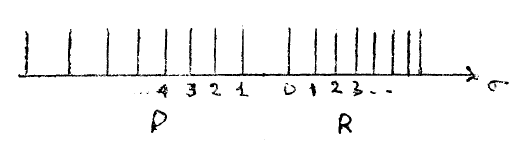
شكل (2)
4- طيوف رامان
الجزئيات ثنائية الذرة متشابهة أو غير متشابهة الذرات لها طيف تشتت رامان اهتزازي - دوراني.
 الاكثر قراءة في الفيزياء الجزيئية
الاكثر قراءة في الفيزياء الجزيئية
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


