


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات Let 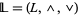 be a lattice, and let
be a lattice, and let 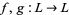 . Then the pair
. Then the pair 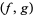 is a local polarity if and only if for each finite set
is a local polarity if and only if for each finite set 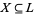 , there is a finitely generated sublattice
, there is a finitely generated sublattice 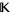 of
of 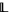 that contains
that contains 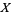 and on which the restriction
and on which the restriction 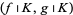 is a lattice polarity.
is a lattice polarity.
Using nonstandard methods, one may show that the following result holds: Let 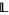 be a locally finite lattice. Then the set of local polarities of
be a locally finite lattice. Then the set of local polarities of 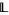 is a relation
is a relation 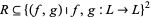 which is a one-to-one correspondence between its domain and range.
which is a one-to-one correspondence between its domain and range.
REFERENCES:
Bandelt, H. H. "Tolerance Relations on Lattices." Bull. Austral. Math. Soc. 23, 367-381, 1981.
Birkhoff, G. Lattice Theory, 3rd ed. Providence, RI: Amer. Math. Soc., 1967.
Chajda, I. and Zelinka, B. "Tolerances and Convexity." Czech. Math. J. 29, 584-587, 1979.
Chajda, I. and Zelinka, B. "A Characterization of Tolerance-Distributive Tree Semilattices." Czech. Math. J. 37, 175-180, 1987.
Grätzer, G. General Lattice Theory, 2nd ed. Boston, MA: Birkhäuser, 1998.
Hobby, D. and McKenzie, R. The Structure of Finite Algebras. Providence, RI: Amer. Math. Soc., 1988.
Insall, M. "Some Finiteness Conditions in Lattices Using Nonstandard Proof Methods." J. Austral. Math. Soc. 53, 266-280, 1992.
Schweigert, D. "Central Relations on Lattices." J. Austral. Math. Soc. 37, 213-219, 1988.
Schweigert, D. and Szymanska, M. "On Central Relations of Complete Lattices." Czech. Math. J. 37, 70-74, 1987.



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|