


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 23-12-2021
Date: 30-12-2021
Date: 4-1-2022
|
The proposal originally made by Georg Cantor that there is no infinite set with a cardinal number between that of the "small" infinite set of integers 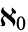 and the "large" infinite set of real numbers
and the "large" infinite set of real numbers 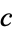 (the "continuum"). Symbolically, the continuum hypothesis is that
(the "continuum"). Symbolically, the continuum hypothesis is that 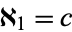 . Problem 1a of Hilbert's problems asks if the continuum hypothesis is true.
. Problem 1a of Hilbert's problems asks if the continuum hypothesis is true.
Gödel showed that no contradiction would arise if the continuum hypothesis were added to conventional Zermelo-Fraenkel set theory. However, using a technique called forcing, Paul Cohen (1963, 1964) proved that no contradiction would arise if the negation of the continuum hypothesis was added to set theory. Together, Gödel's and Cohen's results established that the validity of the continuum hypothesis depends on the version of set theory being used, and is therefore undecidable (assuming the Zermelo-Fraenkel axioms together with the axiom of choice).
Conway and Guy (1996, p. 282) recount a generalized version of the continuum hypothesis originally due to Hausdorff in 1908 which is also undecidable: is 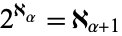 for every
for every 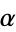 ? The continuum hypothesis follows from generalized continuum hypothesis, so
? The continuum hypothesis follows from generalized continuum hypothesis, so 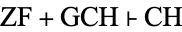 .
.
Woodin (2001ab, 2002) formulated a new plausible "axiom" whose adoption (in addition to the Zermelo-Fraenkel axioms and axiom of choice) would imply that the continuum hypothesis is false. Since set theoreticians have felt for some time that the Continuum Hypothesis should be false, if Woodin's axiom proves to be particularly elegant, useful, or intuitive, it may catch on. It is interesting to compare this to a situation with Euclid's parallel postulate more than 300 years ago, when Wallis proposed an additional axiom that would imply the parallel postulate (Greenberg 1994, pp. 152-153).
REFERENCES:
Cohen, P. J. "The Independence of the Continuum Hypothesis." Proc. Nat. Acad. Sci. U. S. A. 50, 1143-1148, 1963.
Cohen, P. J. "The Independence of the Continuum Hypothesis. II." Proc. Nat. Acad. Sci. U. S. A. 51, 105-110, 1964.
Cohen, P. J. Set Theory and the Continuum Hypothesis. New York: W. A. Benjamin, 1966.
Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, p. 282, 1996.
Ferreirós, J. "The Notion of Cardinality and the Continuum Hypothesis." Ch. 6 in Labyrinth of Thought: A History of Set Theory and Its Role in Modern Mathematics. Basel, Switzerland: Birkhäuser, pp. 171-214, 1999.
Gödel, K. The Consistency of the Continuum-Hypothesis. Princeton, NJ: Princeton University Press, 1940.
Greenberg, M. J. Euclidean and Non-Euclidean Geometries: Development and History, 3rd ed. San Francisco, CA: W. H. Freeman, 1994.
Hoffman, P. The Man Who Loved Only Numbers: The Story of Paul Erdős and the Search for Mathematical Truth. New York: Hyperion, pp. 225-226, 1998.
Jech, T. J. Set Theory, 2nd ed. Berlin: Springer-Verlag, 1997.
McGough, N. "The Continuum Hypothesis." http://www.ii.com/math/ch/.
Woodin, H "The Continuum Hypothesis. Part I." Not. Amer. Math. Soc. 48, 567-576, 2001a.
Woodin, H "The Continuum Hypothesis. Part II." Not. Amer. Math. Soc. 48, 681-690, 2001b.
Woodin, H "Correction to: The Continuum Hypothesis. Part II." Not. Amer. Math. Soc. 49, 46, 2002.



|
|
|
|
4 أسباب تجعلك تضيف الزنجبيل إلى طعامك.. تعرف عليها
|
|
|
|
|
|
|
أكبر محطة للطاقة الكهرومائية في بريطانيا تستعد للانطلاق
|
|
|
|
|
|
|
أصواتٌ قرآنية واعدة .. أكثر من 80 برعماً يشارك في المحفل القرآني الرمضاني بالصحن الحيدري الشريف
|
|
|