المرجع الالكتروني للمعلوماتية
المرجع الألكتروني للمعلوماتية
ENGLISH
آخر المواضيع المضافة

الرياضيات
عدد المواضيع في هذا القسم 9761 موضوعاً
تاريخ الرياضيات
الرياضيات المتقطعة
الجبر
الضبابية
نظرية المجموعات
نظرية الزمر
نظرية الحلقات والحقول
نظرية الاعداد
نظرية الفئات
حساب المتجهات
المتتاليات-المتسلسلات
المصفوفات و نظريتها
المثلثات
الهندسة
التفاضل و التكامل
المعادلات التفاضلية و التكاملية
التحليل
التبلوجيا
نظرية الالعاب
الاحتمالات و الاحصاء
نظرية التحكم
بحوث العمليات
نظرية الكم
الشفرات
الرياضيات التطبيقية
نظريات ومبرهنات
علماء الرياضيات
الرياضيات في العلوم الاخرى
بحوث و اطاريح جامعية
هل تعلم
طرائق التدريس
الرياضيات العامة
نظرية البيان

Untitled Document
أبحث عن شيء أخر المرجع الالكتروني للمعلوماتية
أضيف حديثاً
تـشكيـل اتـجاهات المـستـهلك والعوامـل المؤثـرة عليـها
2024-11-27
النـماذج النـظريـة لاتـجاهـات المـستـهلـك
2024-11-27
{اصبروا وصابروا ورابطوا }
2024-11-27
الله لا يضيع اجر عامل
2024-11-27
ذكر الله
2024-11-27
الاختبار في ذبل الأموال والأنفس
2024-11-27

وثائقيات
العباءة العربية .. إرث الآباء واعتزاز الأبناء
التاريخ / 20-09-2024

مختارات
التخصيص
10-9-2016
مواد العزل للرطوبة - مواد عازلة مرنة Flexible Materials
2023-05-28
الملبدات الحيوية Bioflocculants
2-8-2017
mellow (adj.)
2023-10-10
عقيدة الشيعة في الأنبياء وكتبهم
13-5-2018
ما هو الجوسيبلور Gossyplure؟
2023-05-11

Bairstow,s Method  
  
407   07:53 مساءً   date: 9-12-2021
Author : Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T
Book or Source : Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press
Page and Part : pp. 277 and 283-284


Read More
Chebyshev-Radau Quadrature
Date: 2-12-2021 493
Descartes, Sign Rule
Date: 10-12-2021 562
Chebyshev Quadrature
Date: 2-12-2021 401

Bairstow's Method

A procedure for finding the quadratic factors for the complex conjugate roots of a polynomial 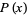P(x) with real coefficients.

[x-(a+ib)][x-(a-ib)]=x^2+2ax+(a^2+b^2)=x^2+Bx+C.

(1)

Now write the original polynomial as

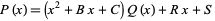P(x)=(x^2+Bx+C)Q(x)+Rx+S

(2)
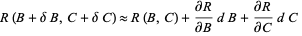R(B+deltaB,C+deltaC) approx R(B,C)+(partialR)/(partialB)dB+(partialR)/(partialC)dC

(3)
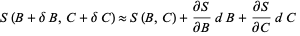S(B+deltaB,C+deltaC) approx S(B,C)+(partialS)/(partialB)dB+(partialS)/(partialC)dC

(4)
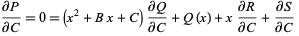(partialP)/(partialC)=0=(x^2+Bx+C)(partialQ)/(partialC)+Q(x)+x(partialR)/(partialC)+(partialS)/(partialC)

(5)
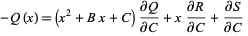-Q(x)=(x^2+Bx+C)(partialQ)/(partialC)+x(partialR)/(partialC)+(partialS)/(partialC)

(6)
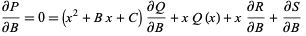(partialP)/(partialB)=0=(x^2+Bx+C)(partialQ)/(partialB)+xQ(x)+x(partialR)/(partialB)+(partialS)/(partialB)

(7)
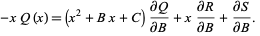-xQ(x)=(x^2+Bx+C)(partialQ)/(partialB)+x(partialR)/(partialB)+(partialS)/(partialB).

(8)

Now use the two-dimensional Newton's method to find the simultaneous solutions.

REFERENCES:

Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T. Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England: Cambridge University Press, pp. 277 and 283-284, 1989.




الجبر أحد الفروع الرئيسية في الرياضيات، حيث إن التمكن من الرياضيات يعتمد على الفهم السليم للجبر. ويستخدم المهندسون والعلماء الجبر يومياً، وتعول المشاريع التجارية والصناعية على الجبر لحل الكثير من المعضلات التي تتعرض لها. ونظراً لأهمية الجبر في الحياة العصرية فإنه يدرّس في المدارس والجامعات في جميع أنحاء العالم. ويُعجب الكثير من الدارسين للجبر بقدرته وفائدته الكبيرتين، إذ باستخدام الجبر يمكن للمرء أن يحل كثيرًا من المسائل التي يتعذر حلها باستخدام الحساب فقط.وجاء اسمه من كتاب عالم الرياضيات والفلك والرحالة محمد بن موسى الخورازمي.


يعتبر علم المثلثات Trigonometry علماً عربياً ، فرياضيو العرب فضلوا علم المثلثات عن علم الفلك كأنهما علمين متداخلين ، ونظموه تنظيماً فيه لكثير من الدقة ، وقد كان اليونان يستعملون وتر CORDE ضعف القوسي قياس الزوايا ، فاستعاض رياضيو العرب عن الوتر بالجيب SINUS فأنت هذه الاستعاضة إلى تسهيل كثير من الاعمال الرياضية.

تعتبر المعادلات التفاضلية خير وسيلة لوصف معظم المـسائل الهندسـية والرياضـية والعلمية على حد سواء، إذ يتضح ذلك جليا في وصف عمليات انتقال الحرارة، جريان الموائـع، الحركة الموجية، الدوائر الإلكترونية فضلاً عن استخدامها في مسائل الهياكل الإنشائية والوصف الرياضي للتفاعلات الكيميائية.
ففي في الرياضيات, يطلق اسم المعادلات التفاضلية على المعادلات التي تحوي مشتقات و تفاضلات لبعض الدوال الرياضية و تظهر فيها بشكل متغيرات المعادلة . و يكون الهدف من حل هذه المعادلات هو إيجاد هذه الدوال الرياضية التي تحقق مشتقات هذه المعادلات.





الأخبار الصحية
"عادة ليلية" قد تكون المفتاح للوقاية من الخرف
التاريخ / 2024-11-26

الأخبار العلمية
ممتص الصدمات: طريقة عمله وأهميته وأبرز علامات تلفه
التاريخ / 2024-11-26

الساحة الاسلامية
المجمع العلمي للقرآن الكريم يقيم جلسة حوارية لطلبة جامعة الكوفة
التاريخ / 2024-11-27