


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 16-2-2016
Date: 11-2-2016
Date: 29-9-2021
|
Consider an 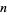 -dimensional deterministic dynamical system
-dimensional deterministic dynamical system
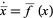 |
and let 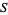 be an
be an 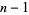 -dimensional surface of section that is traverse to the flow, i.e., all trajectories starting from
-dimensional surface of section that is traverse to the flow, i.e., all trajectories starting from 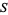 flow through it and are not parallel to it. Then a Poincaré map
flow through it and are not parallel to it. Then a Poincaré map 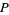 is a mapping from
is a mapping from 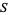 to itself obtained by following trajectories from one intersection of the surface
to itself obtained by following trajectories from one intersection of the surface 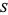 to the next. Poincaré maps are useful when studying swirling flows near periodic solutions in dynamical systems.
to the next. Poincaré maps are useful when studying swirling flows near periodic solutions in dynamical systems.
REFERENCES:
Devaney, R. L. An Introduction to Chaotic Dynamical Systems, 2nd ed. Westview Press, 2003.
Gleick, J. Chaos: Making a New Science. New York: Penguin Books, p. 142, 1988.
Rasband, S. N. "The Poincaré Map." §5.3 in Chaotic Dynamics of Nonlinear Systems. New York: Wiley, pp. 92-95, 1990.
Strogatz, S. H. Nonlinear Dynamics and Chaos. Perseus Books, 1994.



|
|
|
|
لخفض ضغط الدم.. دراسة تحدد "تمارين مهمة"
|
|
|
|
|
|
|
طال انتظارها.. ميزة جديدة من "واتساب" تعزز الخصوصية
|
|
|
|
|
|
|
عوائل الشهداء: العتبة العباسية المقدسة سبّاقة في استذكار شهداء العراق عبر فعالياتها وأنشطتها المختلفة
|
|
|