Similarity Transformation

The term "similarity transformation" is used either to refer to a geometric similarity, or to a matrix transformation that results in a similarity.

A similarity transformation is a conformal mapping whose transformation matrix 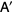 can be written in the form

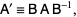(1)

where 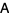 and 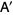 are called similar matrices (Golub and Van Loan 1996, p. 311). Similarity transformations transform objects in space to similar objects. Similarity transformations and the concept of self-similarity are important foundations of fractals and iterated function systems.

The determinant of the similarity transformation of a matrix is equal to the determinant of the original matrix

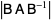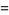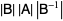			(2)
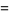			(3)
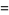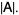			(4)

The determinant of a similarity transformation minus a multiple of the unit matrix is given by

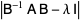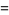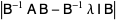			(5)
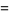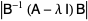			(6)
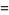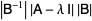			(7)
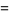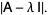			(8)

If 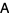 is an antisymmetric matrix (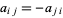) and 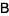 is an orthogonal matrix (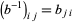), then the matrix for the similarity transformation

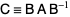(9)

is itself antisymmetric, i.e., 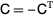. This follows using index notation for matrix multiplication, which gives

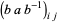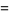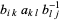			(10)
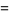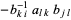			(11)
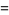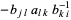			(12)
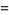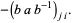			(13)

Here, equation (10) follows from the definition of matrix multiplication, (11) uses the properties of antisymmetry in 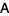 and orthogonality in 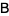, (12) is a rearrangement of (11) allowed since scalar multiplication is commutative, and (13) follows again from the definition of matrix multiplication.

The similarity transformation of a subgroup 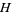 of a group  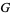by a fixed element  in 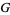 not in  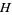always gives a subgroup (Arfken 1985, p. 242).

REFERENCES:

Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, 1985.

Croft, H. T.; Falconer, K. J.; and Guy, R. K. Unsolved Problems in Geometry. New York: Springer-Verlag, p. 3, 1991.

Golub, G. H. and Van Loan, C. F. Matrix Computations, 3rd ed. Baltimore, MD: Johns Hopkins University Press, p. 311, 1996.

Lauwerier, H. Fractals: Endlessly Repeated Geometric Figures. Princeton, NJ: Princeton University Press, pp. 83-103, 1991.