


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 30-9-2021
Date: 29-11-2021
Date: 16-10-2021
|

The Hilbert curve is a Lindenmayer system invented by Hilbert (1891) whose limit is a plane-filling function which fills a square. Traversing the polyhedron vertices of an  -dimensional hypercube in Gray code order produces a generator for the
-dimensional hypercube in Gray code order produces a generator for the  -dimensional Hilbert curve. The Hilbert curve can be simply encoded with initial string "L", string rewriting rules "L" -> "+RF-LFL-FR+", "R" -> "-LF+RFR+FL-", and angle
-dimensional Hilbert curve. The Hilbert curve can be simply encoded with initial string "L", string rewriting rules "L" -> "+RF-LFL-FR+", "R" -> "-LF+RFR+FL-", and angle  (Peitgen and Saupe 1988, p. 278). The
(Peitgen and Saupe 1988, p. 278). The  th iteration of this Hilbert curve is implemented in the Wolfram Language as HilbertCurve[n].
th iteration of this Hilbert curve is implemented in the Wolfram Language as HilbertCurve[n].

A related curve is the Hilbert II curve, shown above (Peitgen and Saupe 1988, p. 284). It is also a Lindenmayer system and the curve can be encoded with initial string "X", string rewriting rules "X" -> "XFYFX+F+YFXFY-F-XFYFX", "Y" -> "YFXFY-F-XFYFX+F+YFXFY", and angle 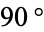 . The
. The 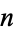 th iteration of this curve is implemented in the Wolfram Language as PeanoCurve[n].
th iteration of this curve is implemented in the Wolfram Language as PeanoCurve[n].

A three-dimensional analog of the Hilbert curve can also be generated (Trott 2004, pp. 93-97).
REFERENCES:
Bogomolny, A. "Plane Filling Curves." http://www.cut-the-knot.org/do_you_know/hilbert.shtml.
Bogomolny, A. "All Peano Curves." http://www.cut-the-knot.org/Curriculum/Geometry/PeanoComplete.shtml.
Charpentier, M. "L-Systems in PostScript." http://www.cs.unh.edu/~charpov/Programming/L-systems/.
Dickau, R. M. "Two-Dimensional L-Systems." http://mathforum.org/advanced/robertd/lsys2d.html.
Dickau, R. M. "Three-Dimensional L-Systems." http://mathforum.org/advanced/robertd/lsys3d.html.
Goetz, P. "Phil Goetz's Complexity Dictionary." http://www.cs.buffalo.edu/~goetz/dict.html
Hilbert, D. "Über die stetige Abbildung einer Linie auf ein Flachenstück." Math. Ann. 38, 459-460, 1891.
Peitgen, H.-O. and Saupe, D. (Eds.). The Science of Fractal Images. New York: Springer-Verlag, pp. 278 and 284, 1988.
Trott, M. The Mathematica GuideBook for Programming. New York: Springer-Verlag, 2004. http://www.mathematicaguidebooks.org/.
Wagon, S. Mathematica in Action. New York: W. H. Freeman, pp. 198-206, 1991.
Wells, D. The Penguin Dictionary of Curious and Interesting Geometry. London: Penguin, pp. 100-101, 1991.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|