


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 20-6-2021
Date: 1-6-2021
Date: 26-9-2016
|

The real projective plane is the closed topological manifold, denoted 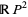 , that is obtained by projecting the points of a plane
, that is obtained by projecting the points of a plane 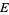 from a fixed point
from a fixed point 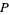 (not on the plane), with the addition of the line at infinity. It can be described by connecting the sides of a square in the orientations illustrated above (Gardner 1971, pp. 15-17; Gray 1997, pp. 323-324).
(not on the plane), with the addition of the line at infinity. It can be described by connecting the sides of a square in the orientations illustrated above (Gardner 1971, pp. 15-17; Gray 1997, pp. 323-324).
There is then a one-to-one correspondence between points in 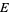 and lines through
and lines through 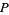 not parallel to
not parallel to 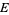 . Lines through
. Lines through 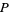 that are parallel to
that are parallel to 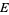 have a one-to-one correspondence with points on the line at infinity. Since each line through
have a one-to-one correspondence with points on the line at infinity. Since each line through 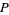 intersects the sphere
intersects the sphere 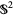 centered at
centered at 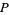 and tangent to
and tangent to 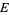 in two antipodal points,
in two antipodal points, 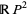 can be described as a quotient space of
can be described as a quotient space of 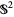 by identifying any two such points. The real projective plane is a nonorientable surface. The equator of
by identifying any two such points. The real projective plane is a nonorientable surface. The equator of 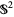 (which, in the quotient space, is itself a projective line) corresponds to the line at infinity.
(which, in the quotient space, is itself a projective line) corresponds to the line at infinity.
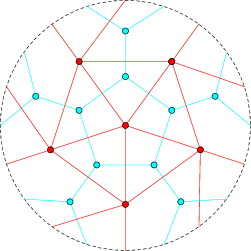
The complete graph on 6 vertices 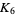 can be drawn in the projective plane without any lines crossing, as illustrated above. Here, the projective plane is shown as a dashed circle, where lines continue on the opposite side of the circle. The dual of
can be drawn in the projective plane without any lines crossing, as illustrated above. Here, the projective plane is shown as a dashed circle, where lines continue on the opposite side of the circle. The dual of 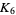 on the projective plane is the Petersen graph.
on the projective plane is the Petersen graph.
The Boy surface, cross-cap, and Roman surface are all homeomorphic to the real projective plane and, because 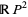 is nonorientable, these surfaces contain self-intersections (Kuiper 1961, Pinkall 1986).
is nonorientable, these surfaces contain self-intersections (Kuiper 1961, Pinkall 1986).
REFERENCES:
Apéry, F. Models of the Real Projective Plane: Computer Graphics of Steiner and Boy Surfaces. Braunschweig, Germany: Vieweg, 1987.
Coxeter, H. S. M. The Real Projective Plane, 3rd ed. Cambridge, England: Cambridge University Press, 1993.
Gardner, M. Martin Gardner's Sixth Book of Mathematical Games from Scientific American. New York: Scribner's, 1971.
Geometry Center. "The Projective Plane." https://www.geom.umn.edu/zoo/toptype/pplane/.
Gray, A. "Realizations of the Real Projective Plane." §14.6 in Modern Differential Geometry of Curves and Surfaces with Mathematica, 2nd ed. Boca Raton, FL: CRC Press, pp. 330-335, 1997.
Klein, F. §1.2 in Vorlesungen über nicht-euklidische Geometrie. New York: Springer-Verlag, 1968.
Kuiper, N. H. "Convex Immersion of Closed Surfaces in 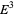 ." Comment. Math. Helv. 35, 85-92, 1961.
." Comment. Math. Helv. 35, 85-92, 1961.
Pinkall, U. Mathematical Models from the Collections of Universities and Museums (Ed. G. Fischer). Braunschweig, Germany: Vieweg, pp. 64-65, 1986.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|