المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Sobolev Space |
 1924
 03:05 مساءً
date: 4-8-2021 |
Author : Mazja, V. 
Book or Source : Sobolev Spaces. New York: Springer-Verlag, 1985. 
Page and Part : ...|
Read More
Date: 1-6-2021
1794
Date: 22-6-2021
3054
Date: 12-8-2021
1661
|
For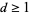 
, 
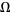an open subset of 
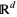, ![p in [1;+infty]](https://mathworld.wolfram.com/images/equations/SobolevSpace/Inline4.gif)
and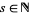 
, the Sobolev space 
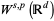is defined by
 |
(1) |
where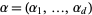 
, 
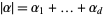, and the derivatives 
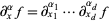are taken in a weak sense.
When endowed with the norm
 |
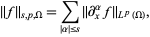(2) |
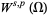is a Banach space.
In the special case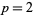 
, 
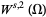is denoted by 
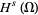. This space is a Hilbert space for the inner product
 |
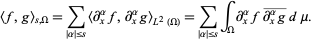(3) |
Sobolev spaces play an important role in the theory of partial differential equations.
REFERENCES:
Mazja, V. Sobolev Spaces. New York: Springer-Verlag, 1985.
|
|
|
|
لخفض ضغط الدم.. دراسة تحدد "تمارين مهمة"
|
|
|
|
|
|
|
طال انتظارها.. ميزة جديدة من "واتساب" تعزز الخصوصية
|
|
|
|
|
|
|
العتبة العباسية المقدسة تطلق فعاليات اليوم الثاني من الحفل المركزي لتخرج طلبة الجامعات
|
|
|
