

تاريخ الرياضيات

الاعداد و نظريتها

تاريخ التحليل

تار يخ الجبر

الهندسة و التبلوجي


الرياضيات في الحضارات المختلفة

العربية

اليونانية

البابلية

الصينية

المايا

المصرية

الهندية


الرياضيات المتقطعة

المنطق

اسس الرياضيات

فلسفة الرياضيات

مواضيع عامة في المنطق


الجبر

الجبر الخطي

الجبر المجرد

الجبر البولياني

مواضيع عامة في الجبر

الضبابية

نظرية المجموعات

نظرية الزمر

نظرية الحلقات والحقول

نظرية الاعداد

نظرية الفئات

حساب المتجهات

المتتاليات-المتسلسلات

المصفوفات و نظريتها

المثلثات


الهندسة

الهندسة المستوية

الهندسة غير المستوية

مواضيع عامة في الهندسة

التفاضل و التكامل


المعادلات التفاضلية و التكاملية

معادلات تفاضلية

معادلات تكاملية

مواضيع عامة في المعادلات


التحليل

التحليل العددي

التحليل العقدي

التحليل الدالي

مواضيع عامة في التحليل

التحليل الحقيقي

التبلوجيا

نظرية الالعاب

الاحتمالات و الاحصاء

نظرية التحكم

بحوث العمليات

نظرية الكم

الشفرات

الرياضيات التطبيقية

نظريات ومبرهنات


علماء الرياضيات

500AD

500-1499

1000to1499

1500to1599

1600to1649

1650to1699

1700to1749

1750to1779

1780to1799

1800to1819

1820to1829

1830to1839

1840to1849

1850to1859

1860to1864

1865to1869

1870to1874

1875to1879

1880to1884

1885to1889

1890to1894

1895to1899

1900to1904

1905to1909

1910to1914

1915to1919

1920to1924

1925to1929

1930to1939

1940to the present

علماء الرياضيات

الرياضيات في العلوم الاخرى

بحوث و اطاريح جامعية

هل تعلم

طرائق التدريس

الرياضيات العامة

نظرية البيان
Möbius Strip
المؤلف:
Ball, W. W. R. and Coxeter, H. S. M
المصدر:
Mathematical Recreations and Essays, 13th ed. New York: Dover
الجزء والصفحة:
...
14-8-2021
6997
Möbius Strip
 |
 |
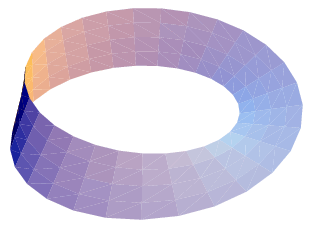
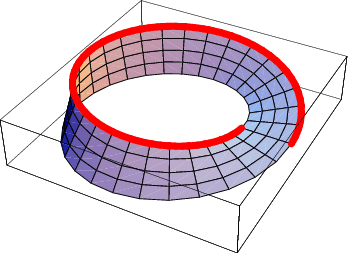
The Möbius strip, also called the twisted cylinder (Henle 1994, p. 110), is a one-sided nonorientable surface obtained by cutting a closed band into a single strip, giving one of the two ends thus produced a half twist, and then reattaching the two ends (right figure; Gray 1997, pp. 322-323). The strip bearing his name was invented by Möbius in 1858, although it was independently discovered by Listing, who published it, while Möbius did not (Derbyshire 2004, p. 381). Like the cylinder, it is not a true surface, but rather a surface with boundary (Henle 1994, p. 110).
The Möbius strip has Euler characteristic 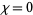 (Dodson and Parker 1997, p. 125).
(Dodson and Parker 1997, p. 125).
According to Madachy (1979), the B. F. Goodrich Company patented a conveyor belt in the form of a Möbius strip which lasts twice as long as conventional belts. M. C. Escher was fond of portraying Möbius strips, and they appear in his woodcuts "Möbius Strip I" and "Möbius Strip II (Red Ants)" (Bool et al. 1982, p. 324; Forty 2003, Plate 70).
A Möbius strip of half-width 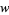 with midcircle of radius
with midcircle of radius 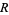 and at height
and at height 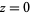 can be represented parametrically by
can be represented parametrically by
 |
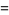 |
![[R+scos(1/2t)]cost](https://mathworld.wolfram.com/images/equations/MoebiusStrip/Inline7.gif) |
(1) |
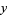 |
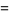 |
![[R+scos(1/2t)]sint](https://mathworld.wolfram.com/images/equations/MoebiusStrip/Inline10.gif) |
(2) |
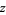 |
 |
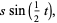 |
(3) |
for ![s in [-w,w]](https://mathworld.wolfram.com/images/equations/MoebiusStrip/Inline14.gif) and
and 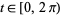 . In this parametrization, the Möbius strip is therefore a cubic surface with equation
. In this parametrization, the Möbius strip is therefore a cubic surface with equation
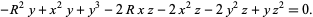 |
(4) |
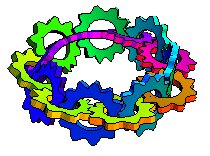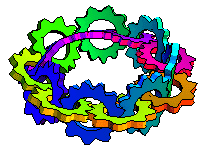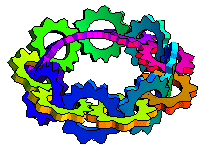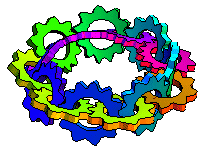
The illustration above shows interlocked turning gears along the length of a Möbius strip (M. Trott, pers. comm., 2001).
The coefficients of the first fundamental form for this surface are
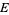 |
 |
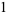 |
(5) |
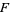 |
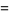 |
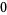 |
(6) |
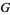 |
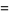 |
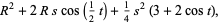 |
(7) |
the second fundamental form coefficients are
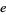 |
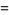 |
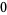 |
(8) |
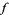 |
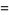 |
![R/(sqrt(4R^2+3s^2+2s[4Rcos(1/2t)+scost]))](https://mathworld.wolfram.com/images/equations/MoebiusStrip/Inline30.gif) |
(9) |
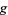 |
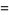 |
![([2(R^2+s^2)+4Rscos(1/2t)+s^2cost]sin(1/2t))/(sqrt(4R^2+3s^2+2s[4Rcos(1/2t)+scost])),](https://mathworld.wolfram.com/images/equations/MoebiusStrip/Inline33.gif) |
(10) |
the area element is
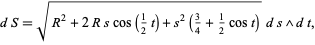 |
(11) |
and the Gaussian and mean curvatures are
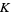 |
 |
(12) |
|
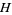 |
 |
(13) |
The perimeter of the Möbius strip is given by integrating the complicated function
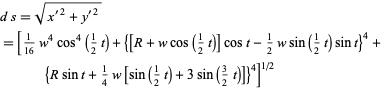 |
(14) |
from 0 to 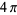 , which can unfortunately not be done in closed form. Note that although the surface closes at
, which can unfortunately not be done in closed form. Note that although the surface closes at 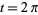 , this corresponds to the bottom edge connecting with the top edge, as illustrated above, so an additional
, this corresponds to the bottom edge connecting with the top edge, as illustrated above, so an additional 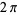 must be traversed to comprise the entire arc length of the bounding edge.
must be traversed to comprise the entire arc length of the bounding edge.
Cutting a Möbius strip, giving it extra twists, and reconnecting the ends produces unexpected figures called paradromic rings (Listing and Tait 1847, Ball and Coxeter 1987) which are summarized in the table below.
| half-twists | cuts | divs. | result |
| 1 | 1 | 2 | 1 band, length 2 |
| 1 | 1 | 3 | 1 band, length 2 |
| 1 Möbius strip, length 1 | |||
| 1 | 2 | 4 | 2 bands, length 2 |
| 1 | 2 | 5 | 2 bands, length 2 |
| 1 Möbius strip, length 1 | |||
| 1 | 3 | 6 | 3 bands, length 2 |
| 1 | 3 | 7 | 3 bands, length 2 |
| 1 Möbius strip, length 1 | |||
| 2 | 1 | 2 | 2 bands, length 1 |
| 2 | 2 | 3 | 3 bands, length 1 |
| 2 | 3 | 4 | 4 bands, length 1 |
A torus can be cut into a Möbius strip with an even number of half-twists, and a Klein bottle can be cut in half along its length to make two Möbius strips. In addition, two strips on top of each other, each with a half-twist, give a single strip with four twists when disentangled.
The topological result of attaching a Möbius strip to a disk along its boundary is a real projective plane, which cannot be embedded in 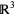 . However, there are three surfaces that are representations of the projective plane in
. However, there are three surfaces that are representations of the projective plane in 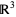 with self-intersections, namely the Boy surface, cross-cap, and Roman surface.
with self-intersections, namely the Boy surface, cross-cap, and Roman surface.
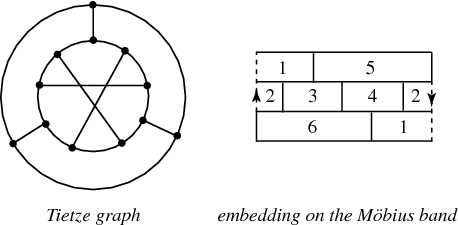
Any set of regions on the Möbius strip can be colored using only six colors, as illustrated in Tietze's graph above.
REFERENCES:
Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, pp. 127-128, 1987.
Bogomolny, A. "Möbius Strip." https://www.cut-the-knot.org/do_you_know/moebius.shtml.
Bondy, J. A. and Murty, U. S. R. Graph Theory with Applications. New York: North Holland, p. 243, 1976.
Bool, F. H.; Kist, J. R.; Locher, J. L.; and Wierda, F. M. C. Escher: His Life and Complete Graphic Work. New York: Abrams, 1982.
Derbyshire, J. Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics. New York: Penguin, 2004.
Dickau, R. "Spinning Möbius Strip Movie." https://mathforum.org/advanced/robertd/moebius.html
Dodson, C. T. J. and Parker, P. E. A User's Guide to Algebraic Topology. Dordrecht, Netherlands: Kluwer, pp. 121 and 284, 1997.
Escher, M. C. "Moebius Strip I." Wood engraving and woodcut in red, green, gold and black, printed from 4 blocks. 1961. https://www.mcescher.com/Gallery/recogn-bmp/LW437.jpg.
Escher, M. C. "Moebius Strip II (Red Ants)." Woodcut in red, black and grey-green, printed from 3 blocks. 1963. https://www.mcescher.com/Gallery/recogn-bmp/LW441.jpg.
Forty, S. M.C. Escher. Cobham, England: TAJ Books, 2003.
Gardner, M. "Möbius Bands." Ch. 9 in Mathematical Magic Show: More Puzzles, Games, Diversions, Illusions and Other Mathematical Sleight-of-Mind from Scientific American. New York: Vintage, pp. 123-136, 1978.
Gardner, M. The Sixth Book of Mathematical Games from Scientific American. Chicago, IL: University of Chicago Press, p. 10, 1984.
Geometry Center. "The Möbius Band." https://www.geom.umn.edu/zoo/features/mobius/.
Gray, A. "The Möbius Strip." §14.3 in Modern Differential Geometry of Curves and Surfaces with Mathematica, 2nd ed. Boca Raton, FL: CRC Press, pp. 325-326, 1997.
Henle, M. A Combinatorial Introduction to Topology. New York: Dover, p. 110, 1994.
Hunter, J. A. H. and Madachy, J. S. Mathematical Diversions. New York: Dover, pp. 41-45, 1975.
JavaView. "Classic Surfaces from Differential Geometry: Moebius Strip." https://www-sfb288.math.tu-berlin.de/vgp/javaview/demo/surface/common/PaSurface_MoebiusStrip.html.
Kraitchik, M. §8.4.3 in Mathematical Recreations. New York: W. W. Norton, pp. 212-213, 1942.
Listing and Tait. Vorstudien zur Topologie, Göttinger Studien, Pt. 10, 1847.
Madachy, J. S. Madachy's Mathematical Recreations. New York: Dover, p. 7, 1979.
Möbius, A. F. Werke, Vol. 2. p. 519, 1858.
Nordstrand, T. "Moebiusband." https://jalape.no/math/moebtxt.
Pappas, T. "The Moebius Strip & the Klein Bottle," "A Twist to the Moebius Strip," "The 'Double' Moebius Strip." The Joy of Mathematics. San Carlos, CA: Wide World Publ./Tetra, p. 207, 1989.
Pickover, C. A. The Möbius Strip: Dr. August Mobius's Marvelous Band in Mathematics, Games, Literature, Art, Technology, and Cosmology. New York: Thunder's Mouth Press, 2006.
Steinhaus, H. Mathematical Snapshots, 3rd ed. New York: Dover, pp. 269-274, 1999.
Trott, M. "The Mathematica Guidebooks Additional Material: Rotating Möbius Bands." https://www.mathematicaguidebooks.org/additions.shtml#G_2_01.
Underwood, M. "Mobius Scarf, Klein Bottle, Klein Bottle 'Hat'." https://www.woolworks.org/patterns/klein.txt.
Wagon, S. "Rotating Circles to Produce a Torus or Möbius Strip." §7.4 in Mathematica in Action. New York: W. H. Freeman, pp. 229-232, 1991.
Wang, P. "Renderings." https://www.ugcs.caltech.edu/~peterw/portfolio/renderings/
Wells, D. The Penguin Dictionary of Curious and Interesting Geometry. London: Penguin, pp. 152-153 and 164, 1991.
 الاكثر قراءة في التبلوجيا
الاكثر قراءة في التبلوجيا
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















