Hilbert Space
المؤلف:
Sansone, G
المصدر:
"Elementary Notions of Hilbert Space." §1.3 in Orthogonal Functions, rev. English ed. New York: Dover
الجزء والصفحة:
...
2-8-2021
2321
Hilbert Space
A Hilbert space is a vector space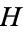 
with an inner product 
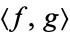such that the norm defined by
turns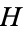 
into a complete metric space. If the metric defined by the norm is not complete, then 
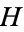is instead known as an inner product space.
Examples of finite-dimensional Hilbert spaces include
1. The real numbers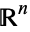 
with 
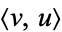the vector dot product of 
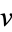and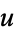 
.
2. The complex numbers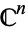 
with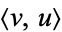 
the vector dot product of 
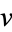and the complex conjugate of 
.
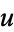An example of an infinite-dimensional Hilbert space is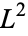 
, the set of all functions 
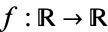such that the integral of 
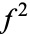over the whole real line is finite. In this case, the inner product is
A Hilbert space is always a Banach space, but the converse need not hold.
A (small) joke told in the hallways of MIT ran, "Do you know Hilbert? No? Then what are you doing in his space?" (S. A. Vaughn, pers. comm., Jul. 31, 2005).
REFERENCES:
Sansone, G. "Elementary Notions of Hilbert Space." §1.3 in Orthogonal Functions, rev. English ed. New York: Dover, pp. 5-10, 1991.
Stone, M. H. Linear Transformations in Hilbert Space and Their Applications Analysis. Providence, RI: Amer. Math. Soc., 1932.
الاكثر قراءة في التبلوجيا
اخر الاخبار
اخبار العتبة العباسية المقدسة
