


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 29-7-2021
Date: 3-8-2021
Date: 2-7-2017
|
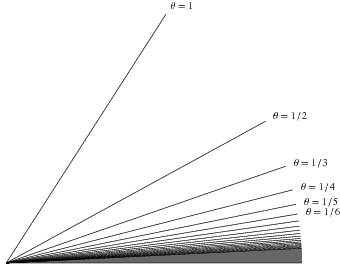
The subset 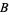 of the Euclidean plane formed by the union of the interval
of the Euclidean plane formed by the union of the interval ![[0,1]](https://mathworld.wolfram.com/images/equations/BroomSpace/Inline2.gif) of the x-axis and all line segments of unit length passing through the origin which form an angle
of the x-axis and all line segments of unit length passing through the origin which form an angle 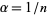 (measured in radians) with it, for all positive integers
(measured in radians) with it, for all positive integers 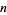 .
.
With respect to the relative topology, 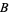 is pathwise-connected. Therefore it is connected, but it is not locally pathwise-connected at any point of the open interval
is pathwise-connected. Therefore it is connected, but it is not locally pathwise-connected at any point of the open interval 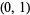 . Each disk centered at one of these points intersects
. Each disk centered at one of these points intersects 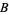 in a union of disjoint segments, which form a disconnected set.
in a union of disjoint segments, which form a disconnected set.
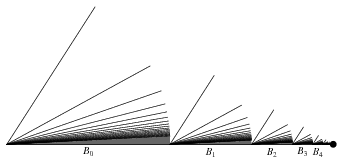
Let 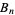 be the broom space formed by segments of length
be the broom space formed by segments of length 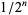 for all natural numbers
for all natural numbers 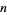 , and place
, and place 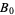 ,
, 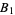 ,
, 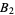 , ... one right after the other on the
, ... one right after the other on the  -axis. This will cover the half-open interval
-axis. This will cover the half-open interval 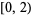 of the
of the  -axis (above figure). The space obtained by adding the point (2,0) to this sequence of brooms is then connected im kleinen at point (2,0), since each open neighborhood of (2,0) contains a closed disk whose radius is exactly formed by the basis intervals of
-axis (above figure). The space obtained by adding the point (2,0) to this sequence of brooms is then connected im kleinen at point (2,0), since each open neighborhood of (2,0) contains a closed disk whose radius is exactly formed by the basis intervals of 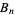 for all sufficiently large
for all sufficiently large 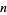 . Hence any two points contained in this disk are connected by a path composed of segments of these broom spaces. On the other hand, point (2, 0) has no connected open neighborhood since every open disk centered at (2,0) has no boundary and hence, unlike in the case of a closed disk, it cannot end right at the vertex of some broom space. Therefore, it must cut through some
. Hence any two points contained in this disk are connected by a path composed of segments of these broom spaces. On the other hand, point (2, 0) has no connected open neighborhood since every open disk centered at (2,0) has no boundary and hence, unlike in the case of a closed disk, it cannot end right at the vertex of some broom space. Therefore, it must cut through some 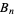 , which will be intersected in an union of disjoint segments, and these form a disconnected set.
, which will be intersected in an union of disjoint segments, and these form a disconnected set.
REFERENCES:
Joshi, K. D. Introduction to General Topology. New Delhi, India: Wiley, p. 157, 1983.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|