The term "continuum" has (at least) two distinct technical meanings in mathematics.

The first is a compact connected metric space (Kuratowski 1968; Lewis 1983, pp. 361-394; Nadler 1992; Prajs and Charatonik).

The second is the nondenumerable set of real numbers, denoted 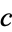. The continuum  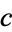satisfies

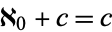(1)

and

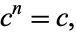(2)

where 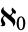 is aleph0 (Aleph-0) and  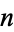is a positive integer. It is also true that

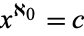(3)

for 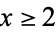. However,

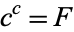(4)

is a set larger than the continuum. Paradoxically, there are exactly as many points 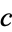 on a line (or line segment) as in a plane, a three-dimensional space, or finite hyperspace, since all these sets can be put into a one-to-one correspondence with each other.

The continuum hypothesis, first proposed by Georg Cantor, holds that the cardinal number of the continuum is the same as that of aleph1. The surprising truth is that this proposition is undecidable, since neither it nor its converse contradicts the tenets of set theory.

REFERENCES:

Kuratowski, K. Topology, Vol. 2. New York: Academic Press, 1968.

Lewis, W. "Continuum Theory Problems." Topology Proc. 8, 361-394, 1983.

Nadler, S. B. Jr. Continuum Theory. New York: Dekker, 1992.

Prajs, J. R. and Charatonik, W. J. (Eds.). "Open Problems in Continuum Theory." https://web.umr.edu/~continua/.

اخر الاخبار

اخبار العتبة العباسية المقدسة

جمعية كشافة الكفيل: المجالس الحسينية تعلّم الفتية قيم نهضة الإمام الحسين (عليه السلام)

عَبرَ المجالس الحسينية.. المجمَع العلمي يقدّم محاضرات دينية وتلاوات قرآنية في بغداد والنجف وميسان

برعاية العتبة العباسية المقدسة.. موكب قناديل السماء يُحيي مراسم اليوم الثالث عشر من المحرّم

بعد انتهاء مراسم ذكرى دفن الأجساد الطاهرة قسم رعاية الصحن يباشر بحملة تنظيف واسعة لصحن مرقد أبي الفضل العباس (عليه السلام)

المزيد

الآخبار الصحية

اختراق علمي.. دواء يؤخر ظهور السكري من النوع الأول لسنوات

هذا ما يحدث لجسمك إن أهملت نظافة فراشك

لماذا تعتبر النساء أكثر عرضة للإصابة بألزهايمر من الرجال؟

لماذا يحذر الخبراء من الإفراط في تناول الفراولة؟

المزيد

الآخبار التكنلوجية

السيارات الكهربائية أنظف بنسبة 73% من سيارات الوقود

سيارة لوسِد الكهربائية تدخل "غينيس" بأطول مدى في العالم

نظرية جديدة تنسف كل ما نعرفه عن تشكل أول قارة في الأرض

منذ 37 ألف عام.. دراسة تكشف "أقدم أمراض" أصابت البشر

المزيد