


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 7-8-2021
Date: 21-6-2017
Date: 5-7-2021
|
Many authors (e.g., Mendelson 1963; Pervin 1964) use the term arcwise-connected as a synonym for pathwise-connected. Other authors (e.g., Armstrong 1983; Cullen 1968; and Kowalsky 1964) use the term to refer to a stronger type of connectedness, namely that an arc connecting two points 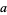 and
and 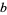 of a topological space
of a topological space 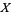 is not simply (like a path) a continuous function
is not simply (like a path) a continuous function ![f:[0,1]->X](https://mathworld.wolfram.com/images/equations/Arcwise-Connected/Inline4.gif) such that
such that 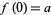 and
and 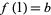 , but must also have a continuous inverse function, i.e., that it is a homeomorphism between
, but must also have a continuous inverse function, i.e., that it is a homeomorphism between ![[0,1]](https://mathworld.wolfram.com/images/equations/Arcwise-Connected/Inline7.gif) and the image of
and the image of 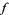 .
.
The difference between the two notions can be clarified by a simple example. The set 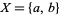 with the trivial topology is pathwise-connected, but not arcwise-connected since the function
with the trivial topology is pathwise-connected, but not arcwise-connected since the function ![f:[0,1]->X](https://mathworld.wolfram.com/images/equations/Arcwise-Connected/Inline10.gif) defined by
defined by 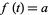 for all
for all 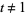 , and
, and 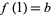 , is a path from
, is a path from 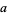 to
to 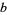 , but there exists no homeomorphism from
, but there exists no homeomorphism from ![[0,1]](https://mathworld.wolfram.com/images/equations/Arcwise-Connected/Inline16.gif) to
to 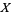 , since even injectivity is impossible.
, since even injectivity is impossible.
Arcwise- and pathwise-connected are equivalent in Euclidean spaces and in all topological spaces having a sufficiently rich structure. In particular theorem states that every locally compact, connected, locally connected metrizable topological space is arcwise-connected (Cullen 1968, p. 327).
REFERENCES:
Armstrong, M. A. Basic Topology, rev. ed. New York: Springer-Verlag, p. 112, 1997.
Cullen, H. F. Introduction to General Topology. Boston, MA: Heath, pp. 325-330, 1968.
Kowalsky, H. J. Topological Spaces. New York: Academic Press, p. 183, 1964.
Mendelson, B. Introduction to Topology. London, England: Blackie & Son, 1963.
Pervin, W. J. "Arcwise Connectivity." §4.5 in Foundations of General Topology. New York: Academic Press, pp. 67-68, 1964.



|
|
|
|
4 أسباب تجعلك تضيف الزنجبيل إلى طعامك.. تعرف عليها
|
|
|
|
|
|
|
أكبر محطة للطاقة الكهرومائية في بريطانيا تستعد للانطلاق
|
|
|
|
|
|
|
العتبة العباسية المقدسة تبحث مع العتبة الحسينية المقدسة التنسيق المشترك لإقامة حفل تخرج طلبة الجامعات
|
|
|