A connex is a geometric form introduced by Clebsch (1872) that included as special cases the curve considered as a point locus and the curve considered as a line envelope (Kasner 1903). Clebsch studied the case 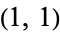, which is equivalent to a collineation, Godt studied the case  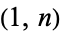(Godt 1873; Clebsch and Lindemann 1876), and Darboux (1878) incompletely investigated the general  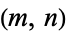case.

The (planar) connex 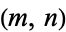 of 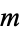th order and 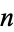th class is represented by an equation of the form

that involves a set of point coordinates and a set of line coordinates, and may be considered as an 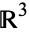 manifold in which each element consists of a point and a line.

An extension of the connex to space was proposed by Krause (1879) who studied the 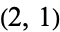 case, and for general  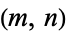by Sintsof (1895, 1898).

REFERENCES:

Clebsch, A. "Ueber ein neues Grundgebilde der analytischen Geometri der Ebene." Göttinger Nachr. No. 22, 1872. Reprinted in Math. Ann. 6, 203-225, 1873.

Clebsch, A. §2 in Vorlesungen über Geometrie, Vol. 1. Leipzig: Teubner, p. 924, 1876.

Darboux, G. "Mémoire sur les équations différentielles algébriques du premier ordre et du premier degré." Bull. Sci. Math. 2, 60-96, 12-144, and 151-200, 1878.

Glenn, O. E. "On the Invariant System of a Pair of Connexes." Trans. Amer. Math. Soc. 17, 405-417, 1916.

Godt. Ueber den Connex erster Ordnung und zweiter Classe. Göttingen, Germany, 1873.

Hirst. Proc. London Math. Soc. 63, 1874.

Kasner, E. "On the Point-Line as Element of Space: A Study of the Corresponding Bilinear Connex." Trans. Amer. Math. Soc. 4, 213-233, 1903.

Krause. "Ueber ein Gebilde der analytischen Geometrie des Raumes, welche dem Connex zweiter Ordnung und erster Classe entspricht." Math. Ann. 14, 294-322, 1879.

Sintsof. Theory of the Connex in Space, in Connection with the Theory of Partial Differential Equations of the First Order. Publications of Kasan University, 1895.

Sintsof. "Theorie des connexes dans l'espace." Bull. des Sci. Math., p. 176, 1898.

Stephanos. Bull. Sci. Math. 4, 1880.

اخر الاخبار

اخبار العتبة العباسية المقدسة

العتبة العباسية المقدسة تواصل تنظيم مجالس العزاء الصباحية بذكرى زيارة عاشوراء

مواكب العزاء تستذكر في التاسع من شهر المحرم شهادة عبدالله الرضيع بن الحسين (عليهما السلام)

العتبة العباسية المقدسة تستذكر تضحيات القاسم بن الحسن (عليهما السلام)

شعبة الحرم الشريف تواصل تنفيذ خطتها الخاصة بشهر المحرّم داخل مرقد أبي الفضل العباس (عليه السلام)

المزيد

الآخبار الصحية

لهذا السبب.. إغلاق 25 مركزًا لعلاج الإدمان في مصر ؟

خلافا للاعتقاد الشائع.. علماء يكشفون أسرار بذور البطيخ ؟!

هذا ما يحدث لجسمك عند تناولك الطماطم بانتظام !

تعرف على أطعمة تسرّع "تعافي الجسم" من حروق الشمس

المزيد

الآخبار التكنلوجية

الثلوج تغطي الصحراء الأكثر جفافا في العالم!

بتلسكوب "ألما".. التقاط صورا غير مسبوقة لبدايات الكون !

هل هاتفك مراقب؟.. 5 علامات خطيرة تكشف التجسس عليك

دبي تطلق أول رحلة تجريبية للتاكسي الجوي

المزيد