


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 3-8-2021
Date: 17-7-2021
Date: 21-7-2021
|
Let 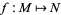 be a map between two compact, connected, oriented
be a map between two compact, connected, oriented 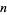 -dimensional manifolds without boundary. Then
-dimensional manifolds without boundary. Then 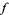 induces a homomorphism
induces a homomorphism 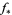 from the homology groups
from the homology groups 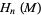 to
to 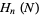 , both canonically isomorphic to the integers, and so
, both canonically isomorphic to the integers, and so 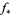 can be thought of as a homomorphism of the integers. The integer
can be thought of as a homomorphism of the integers. The integer 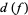 to which the number 1 gets sent is called the degree of the map
to which the number 1 gets sent is called the degree of the map 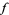 .
.
There is an easy way to compute 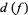 if the manifolds involved are smooth. Let
if the manifolds involved are smooth. Let 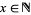 , and approximate
, and approximate 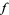 by a smooth map homotopic to
by a smooth map homotopic to 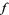 such that
such that  is a "regular value" of
is a "regular value" of 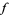 (which exist and are everywhere dense by Sard's theorem). By the implicit function theorem, each point in
(which exist and are everywhere dense by Sard's theorem). By the implicit function theorem, each point in 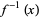 has a neighborhood such that
has a neighborhood such that 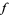 restricted to it is a diffeomorphism. If the diffeomorphism is orientation preserving, assign it the number
restricted to it is a diffeomorphism. If the diffeomorphism is orientation preserving, assign it the number 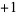 , and if it is orientation reversing, assign it the number
, and if it is orientation reversing, assign it the number 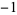 . Add up all the numbers for all the points in
. Add up all the numbers for all the points in 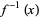 , and that is the
, and that is the 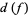 , the Brouwer degree of
, the Brouwer degree of 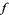 . One reason why the degree of a map is important is because it is a homotopy invariant. A sharper result states that two self-maps of the
. One reason why the degree of a map is important is because it is a homotopy invariant. A sharper result states that two self-maps of the 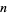 -sphere are homotopic iff they have the same degree. This is equivalent to the result that the
-sphere are homotopic iff they have the same degree. This is equivalent to the result that the 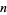 th homotopy group of the
th homotopy group of the 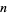 -sphere is the set
-sphere is the set 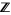 of integers. The isomorphism is given by taking the degree of any representation.
of integers. The isomorphism is given by taking the degree of any representation.
One important application of the degree concept is that homotopy classes of maps from 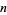 -spheres to
-spheres to 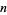 -spheres are classified by their degree (there is exactly one homotopy class of maps for every integer
-spheres are classified by their degree (there is exactly one homotopy class of maps for every integer 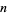 , and
, and 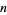 is the degree of those maps).
is the degree of those maps).
REFERENCES:
Drábek, P. and Milota, J. "Brouwer Degree." §4.3D in Methods of Nonlinear Analysis: Applications to Differential Equations. Basel, Switzerland: Birkhäuser, pp. 228-248, 2007.
Milnor, J. W. Topology from the Differentiable Viewpoint. Princeton, NJ: Princeton University Press, pp. 27-31, 1965.



|
|
|
|
لخفض ضغط الدم.. دراسة تحدد "تمارين مهمة"
|
|
|
|
|
|
|
طال انتظارها.. ميزة جديدة من "واتساب" تعزز الخصوصية
|
|
|
|
|
|
|
مشاتل الكفيل تزيّن مجمّع أبي الفضل العبّاس (عليه السلام) بالورد استعدادًا لحفل التخرج المركزي
|
|
|