


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 28-6-2017
Date: 12-6-2021
Date: 29-7-2021
|
Let 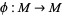 be a
be a 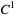 diffeomorphism on a compact Riemannian manifold
diffeomorphism on a compact Riemannian manifold 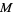 . Then
. Then 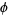 satisfies Axiom A if the nonwandering set
satisfies Axiom A if the nonwandering set 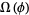 of
of 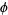 is hyperbolic and the periodic points of
is hyperbolic and the periodic points of 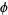 are dense in
are dense in 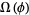 . Although it was conjectured that the first of these conditions implies the second, they were shown to be independent in or around 1977. Examples include the Anosov diffeomorphisms and Smale horseshoe map.
. Although it was conjectured that the first of these conditions implies the second, they were shown to be independent in or around 1977. Examples include the Anosov diffeomorphisms and Smale horseshoe map.
In some cases, Axiom A can be replaced by the condition that the diffeomorphism is a hyperbolic diffeomorphism on a hyperbolic set (Bowen 1975, Parry and Pollicott 1990).
REFERENCES:
Bowen, R. Equilibrium States and the Ergodic Theory of Anosov Diffeomorphisms. New York: Springer-Verlag, 1975.
Ott, E. Chaos in Dynamical Systems. New York: Cambridge University Press, p. 143, 1993.
Parry, W. and Pollicott, M. "Zeta Functions and the Periodic Orbit Structure of Hyperbolic Dynamics." Astérisque No. 187-188, 1990.
Smale, S. "Differentiable Dynamical Systems." Bull. Amer. Math. Soc. 73, 747-817, 1967.



|
|
|
|
4 أسباب تجعلك تضيف الزنجبيل إلى طعامك.. تعرف عليها
|
|
|
|
|
|
|
أكبر محطة للطاقة الكهرومائية في بريطانيا تستعد للانطلاق
|
|
|
|
|
|
|
مركز الكفيل يباشر بتنفيذ الأعمال الطباعية الخاصّة بحفل تخرّج طلبة الجامعات العراقية
|
|
|