


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 12-5-2021
Date: 7-8-2021
Date: 27-5-2021
|
An alternating knot is a knot which possesses a knot diagram in which crossings alternate between under- and overpasses. Not all knot diagrams of alternating knots need be alternating diagrams.
The trefoil knot and figure eight knot are alternating knots, as are all prime knots with seven or fewer crossings. A knot can be checked in the Wolfram Language to see if it is alternating using KnotData[knot, "Alternating"].
The number of prime alternating and nonalternating knots of 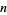 crossings are summarized in the following table.
crossings are summarized in the following table.
| type | OEIS | counts |
| alternating | A002864 | 0, 0, 1, 1, 2, 3, 7, 18, 41, 123, 367, 1288, 4878, 19536, 85263, 379799, ... |
| nonalternating | A051763 | 0, 0, 0, 0, 0, 0, 0, 3, 8, 42, 185, 888, 5110, 27436, 168030, 1008906, ... |

The 3 nonalternating knots of eight crossings are 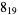 ,
, 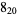 , and
, and 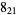 , illustrated above (Wells 1991).
, illustrated above (Wells 1991).
One of Tait's knot conjectures states that the number of crossings is the same for any diagram of a reduced alternating knot. Furthermore, a reduced alternating projection of a knot has the least number of crossings for any projection of that knot. Both of these facts were proved true by Kauffman (1988), Thistlethwaite (1987), and Murasugi (1987). Flype moves are sufficient to pass between all minimal diagrams of a given alternating knot (Hoste et al. 1998).
If 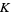 has a reduced alternating projection of
has a reduced alternating projection of 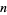 crossings, then the link span of
crossings, then the link span of 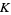 is
is 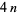 . Let
. Let 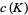 be the link crossing number. Then an alternating knot
be the link crossing number. Then an alternating knot 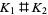 (a knot sum) satisfies
(a knot sum) satisfies
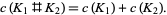 |
In fact, this is true as well for the larger class of adequate knots and postulated for all knots.
It is conjectured that the proportion of knots which are alternating tends exponentially to zero with increasing crossing number (Hoste et al. 1998), a statement which has been proved true for alternating links.
REFERENCES:
Adams, C. C. The Knot Book: An Elementary Introduction to the Mathematical Theory of Knots. New York: W. H. Freeman, pp. 159-164, 1994.
Arnold, B.; Au, M.; Candy, C.; Erdener, K.; Fan, J.; Flynn, R.; Muir, J.; Wu, D.; and Hoste, J. "Tabulating Alternating Knots through 14 Crossings." ftp://chs.cusd.claremont.edu/pub/knot/paper.TeX.txt.
Arnold, B.; Au, M.; Candy, C.; Erdener, K.; Fan, J.; Flynn, R.; Muir, J.; Wu, D.; and Hoste, J. ftp://chs.cusd.claremont.edu/pub/knot/AltKnots/.
Erdener, K. and Flynn, R. "Rolfsen's Table of all Alternating Diagrams through 9 Crossings." ftp://chs.cusd.claremont.edu/pub/knot/Rolfsen_table.final.
Hoste, J.; Thistlethwaite, M.; and Weeks, J. "The First 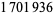 Knots." Math. Intell. 20, 33-48, Fall 1998.
Knots." Math. Intell. 20, 33-48, Fall 1998.
Kauffman, L. "New Invariants in the Theory of Knots." Amer. Math. Monthly 95, 195-242, 1988.
Little, C. N. "Non Alternate 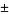 Knots of Orders Eight and Nine." Trans. Roy. Soc. Edinburgh 35, 663-664, 1889.
Knots of Orders Eight and Nine." Trans. Roy. Soc. Edinburgh 35, 663-664, 1889.
Little, C. N. "Alternate 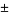 Knots of Order 11." Trans. Roy. Soc. Edinburgh 36, 253-255, 1890.
Knots of Order 11." Trans. Roy. Soc. Edinburgh 36, 253-255, 1890.
Little, C. N. "Non-Alternate 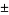 Knots." Trans. Roy. Soc. Edinburgh 39, 771-778, 1900.
Knots." Trans. Roy. Soc. Edinburgh 39, 771-778, 1900.
Livingston, C. Knot Theory. Washington, DC: Math. Assoc. Amer., pp. 6, 132, and 219, 1993.
Murasugi, K. "Jones Polynomials and Classical Conjectures in Knot Theory." Topology 26, 297-307, 1987.
Sloane, N. J. A. Sequences A002864/M0847 and A051763 in "The On-Line Encyclopedia of Integer Sequences."
Thistlethwaite, M. "A Spanning Tree Expansion for the Jones Polynomial." Topology 26, 297-309, 1987.
Wells, D. The Penguin Dictionary of Curious and Interesting Geometry. London: Penguin, p. 160, 1991.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|