


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 27-5-2021
Date: 17-7-2021
Date: 13-6-2021
|
A topologically invariant property of a surface defined as the largest number of nonintersecting simple closed curves that can be drawn on the surface without separating it. Roughly speaking, it is the number of holes in a surface.
The genus of a surface, also called the geometric genus, is related to the Euler characteristic 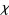 . For a orientable surface such as a sphere (genus 0) or torus (genus 1), the relationship is
. For a orientable surface such as a sphere (genus 0) or torus (genus 1), the relationship is
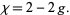 |
For a nonorientable surface such as a real projective plane (genus 1) or Klein bottle (genus 2), the relationship is
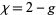 |
(Massey 2003).
REFERENCES:
Gray, A. Modern Differential Geometry of Curves and Surfaces with Mathematica, 2nd ed. Boca Raton, FL: CRC Press, p. 635, 1997.
Massey, W. S. A Basic Course in Algebraic Topology. New York: Springer-Verlag, p. 30, 1997.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|