


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 29-7-2021
Date: 19-6-2021
Date: 8-8-2021
|
Let a closed surface have genus 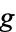 . Then the polyhedral formula generalizes to the Poincaré formula
. Then the polyhedral formula generalizes to the Poincaré formula
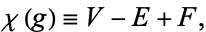 |
(1) |
where
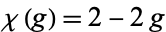 |
(2) |
is the Euler characteristic, sometimes also known as the Euler-Poincaré characteristic. The polyhedral formula corresponds to the special case 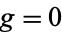 .
.
The only compact closed surfaces with Euler characteristic 0 are the Klein bottle and torus (Dodson and Parker 1997, p. 125). The following table gives the Euler characteristics for some common surfaces (Henle 1994, pp. 167 and 295; Alexandroff 1998, p. 99).
| surface | 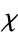 |
| cylinder | 0 |
| double torus | 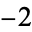 |
| Klein bottle | 0 |
| Möbius strip | 0 |
| projective plane | 1 |
| sphere | 2 |
| torus | 0 |
In terms of the integral curvature of the surface 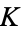 ,
,
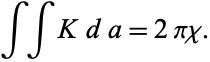 |
(3) |
The Euler characteristic is sometimes also called the Euler number. It can also be expressed as
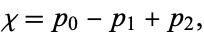 |
(4) |
where 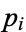 is the
is the 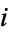 th Betti number of the space.
th Betti number of the space.
REFERENCES:
Alexandroff, P. S. Combinatorial Topology. New York: Dover, 1998.
Armstrong, M. A. "Euler Characteristics." §7.3 in Basic Topology, rev. ed. New York: Springer-Verlag, pp. 158-161, 1997 Coxeter, H. S. M. "Poincaré's Proof of Euler's Formula." Ch. 9 in Regular Polytopes, 3rd ed. New York: Dover, pp. 165-172, 1973.
Dodson, C. T. J. and Parker, P. E. A User's Guide to Algebraic Topology. Dordrecht, Netherlands: Kluwer, 1997.
Gray, A. Modern Differential Geometry of Curves and Surfaces with Mathematica, 2nd ed. Boca Raton, FL: CRC Press, p. 635, 1997.
Henle, M. A Combinatorial Introduction to Topology. New York: Dover, p. 167, 1994.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
العتبة العباسية المقدسة تستعد لإطلاق الحفل المركزي لتخرج طلبة الجامعات العراقية
|
|
|