
Simplicial Complex
 المؤلف:
Harary, F.
المؤلف:
Harary, F.
 المصدر:
Graph Theory. Reading, MA: Addison-Wesley
المصدر:
Graph Theory. Reading, MA: Addison-Wesley
 الجزء والصفحة:
...
الجزء والصفحة:
...
 17-5-2021
17-5-2021
 2246
2246
Simplicial Complex

A simplicial complex is a space with a triangulation. Formally, a simplicial complex 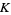 in
in 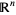 is a collection of simplices in
is a collection of simplices in 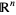 such that
such that
1. Every face of a simplex of 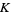 is in
is in 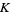 , and
, and
2. The intersection of any two simplices of 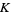 is a face of each of them
is a face of each of them
(Munkres 1993, p. 7).
Objects in the space made up of only the simplices in the triangulation of the space are called simplicial subcomplexes. When only simplicial complexes and simplicial subcomplexes are considered, defining homology is particularly easy (and, in fact, combinatorial because of its finite/counting nature). This kind of homology is called simplicial homology.
REFERENCES:
Harary, F. Graph Theory. Reading, MA: Addison-Wesley, p. 7, 1994.
Hatcher, A. Algebraic Topology. Cambridge, England: Cambridge University Press, 2002.
Munkres, J. R. "Simplicial Complexes and Simplicial Maps." §1.2 in Elements of Algebraic Topology. New York: Perseus Books Pub.,pp. 7-14, 1993.
 الاكثر قراءة في التبلوجيا
الاكثر قراءة في التبلوجيا
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


