


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 21-6-2017
Date: 21-6-2021
Date: 19-6-2021
|
A CW-complex is a homotopy-theoretic generalization of the notion of a simplicial complex. A CW-complex is any space 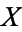 which can be built by starting off with a discrete collection of points called
which can be built by starting off with a discrete collection of points called 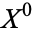 , then attaching one-dimensional disks
, then attaching one-dimensional disks 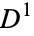 to
to 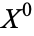 along their boundaries
along their boundaries 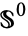 , writing
, writing 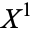 for the object obtained by attaching the
for the object obtained by attaching the 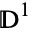 s to
s to 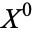 , then attaching two-dimensional disks
, then attaching two-dimensional disks 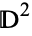 to
to 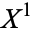 along their boundaries
along their boundaries 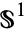 , writing
, writing 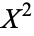 for the new space, and so on, giving spaces
for the new space, and so on, giving spaces 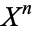 for every
for every 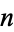 . A CW-complex is any space that has this sort of decomposition into subspaces
. A CW-complex is any space that has this sort of decomposition into subspaces 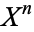 built up in such a hierarchical fashion (so the
built up in such a hierarchical fashion (so the 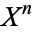 s must exhaust all of
s must exhaust all of 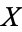 ). In particular,
). In particular, 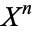 may be built from
may be built from 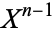 by attaching infinitely many
by attaching infinitely many 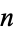 -disks, and the attaching maps
-disks, and the attaching maps 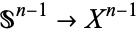 may be any continuous maps.
may be any continuous maps.
The main importance of CW-complexes is that, for the sake of homotopy, homology, and cohomology groups, every space is a CW-complex. This is called the CW-approximation theorem. Another is Whitehead's theorem, which says that maps between CW-complexes that induce isomorphisms on all homotopy groups are actually homotopy equivalences.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|