


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 20-4-2021
Date: 30-3-2021
Date: 15-2-2016
|
A system of equation types obtained by generalizing the differential equation for the normal distribution
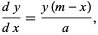 |
(1) |
which has solution
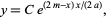 |
(2) |
to
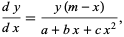 |
(3) |
which has solution
![y=C(a+bx+cx^2)^(-1/(2c))exp[((b+2cm)tan^(-1)((b+2cx)/(sqrt(4ac-b^2))))/(csqrt(4ac-b^2))].](https://mathworld.wolfram.com/images/equations/PearsonSystem/NumberedEquation4.gif) |
(4) |
Let 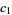 ,
, 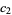 be the roots of
be the roots of 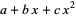 . Then the possible types of curves are
. Then the possible types of curves are
0. 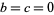 ,
, 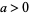 . E.g., normal distribution.
. E.g., normal distribution.
I. 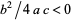 ,
, 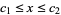 . E.g., beta distribution.
. E.g., beta distribution.
II. 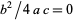 ,
, 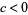 ,
, 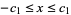 where
where 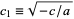 .
.
III. 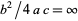 ,
, 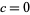 ,
, 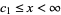 where
where 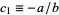 . E.g., gamma distribution. This case is intermediate to cases I and VI.
. E.g., gamma distribution. This case is intermediate to cases I and VI.
IV. 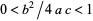 ,
, 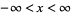 .
.
V. 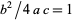 ,
, 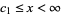 where
where 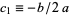 . Intermediate to cases IV and VI.
. Intermediate to cases IV and VI.
VI. 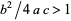 ,
, 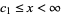 where
where 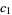 is the larger root. E.g., beta prime distribution.
is the larger root. E.g., beta prime distribution.
VII. 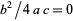 ,
, 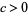 ,
, 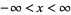 . E.g., Student's t-distribution.
. E.g., Student's t-distribution.
Classes IX-XII are discussed in Pearson (1916). See also Craig (in Kenney and Keeping 1951).
If a Pearson curve possesses a mode, it will be at 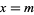 . Let
. Let 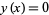 at
at 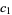 and
and 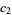 , where these may be
, where these may be  or
or  . If
. If 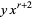 also vanishes at
also vanishes at 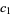 ,
, 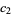 , then the
, then the 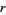 th moment and
th moment and 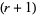 th moments exist.
th moments exist.
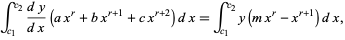 |
(5) |
giving
![[y(ax^r+bx^(r+1)+cx^(r+2))]_(c_1)^(c_2)-int_(c_1)^(c_2)y[arx^(r-1)+b(r+1)x^r+c(r+2)x^(r+1)]dx
=int_(c_1)^(c_2)y(mx^r-x^(r+1))dx](https://mathworld.wolfram.com/images/equations/PearsonSystem/NumberedEquation6.gif) |
(6) |
![0-int_(c_1)^(c_2)y[arx^(r-1)+b(r+1)x^r+c(r+2)x^(r+1)]dx=int_(c_1)^(c_2)y(mx^r-x^(r+1))dx.](https://mathworld.wolfram.com/images/equations/PearsonSystem/NumberedEquation7.gif) |
(7) |
Now define the raw 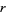 th moment by
th moment by
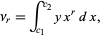 |
(8) |
so combining (7) with (8) gives
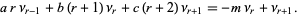 |
(9) |
For 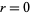 ,
,
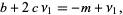 |
(10) |
so
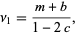 |
(11) |
and for 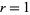 ,
,
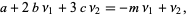 |
(12) |
so
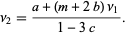 |
(13) |
Combining (11), (13), and the definitions
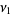 |
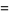 |
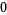 |
(14) |
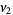 |
 |
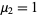 |
(15) |
obtained by letting 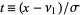 and solving simultaneously gives
and solving simultaneously gives 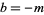 and
and 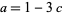 . Writing
. Writing
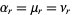 |
(16) |
then allows the general recurrence to be written
![(1-3c)ralpha_(r-1)-mralpha_r+[c(r+2)-1]alpha_(r+1)=0.](https://mathworld.wolfram.com/images/equations/PearsonSystem/NumberedEquation15.gif) |
(17) |
For the special cases 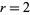 and
and 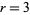 , this gives
, this gives
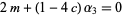 |
(18) |
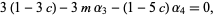 |
(19) |
so the skewness and kurtosis excess are
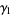 |
 |
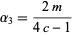 |
(20) |
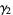 |
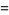 |
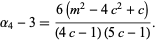 |
(21) |
The parameters 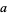 ,
, 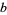 , and
, and 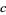 can therefore be written
can therefore be written
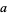 |
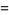 |
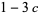 |
(22) |
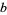 |
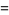 |
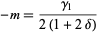 |
(23) |
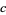 |
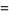 |
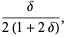 |
(24) |
where
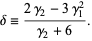 |
(25) |
REFERENCES:
Craig, C. C. "A New Exposition and Chart for the Pearson System of Frequency Curves." Ann. Math. Stat. 7, 16-28, 1936.
Kenney, J. F. and Keeping, E. S. Mathematics of Statistics, Pt. 2, 2nd ed. Princeton, NJ: Van Nostrand, p. 107, 1951.
Pearson, K. "Second Supplement to a Memoir on Skew Variation." Phil. Trans. A 216, 429-457, 1916.



|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
المجمع العلمي ينظّم ندوة حوارية حول مفهوم العولمة الرقمية في بابل
|
|
|