المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Quantile Function |
 1541
 12:03 صباحاً
date: 15-3-2021 |
Author : Shaw, W. 
Book or Source : Refinement of the Normal Quantile: A Benchmark Normal Quantile Based on Recursion, and an Appraisal of the Beasley-Springer-Moro, Acklam, and Wichura... 
Page and Part : ...|
Read More
Date: 10-4-2021
1439
Date: 16-3-2021
1130
Date: 9-3-2021
1343
|
Given a random variable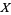 
with continuous and strictly monotonic probability density function 
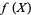, a quantile function 
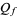assigns to each probability 
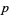attained by 
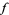the value 
for which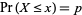 
. Symbolically,
 |
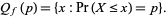Defining quantile functions for discrete rather than continuous distributions requires a bit more work since the discrete nature of such a distribution means that there may be gaps between values in the domain of the distribution function and/or "plateaus" in its range. Therefore, one often defines the associated quantile function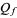 
to be
 |
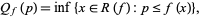where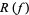 
denotes the range of 
.
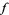REFERENCES:
Shaw, W. "Refinement of the Normal Quantile: A Benchmark Normal Quantile Based on Recursion, and an Appraisal of the Beasley-Springer-Moro, Acklam, and Wichura (AS241) Methods." 2007. https://www.mth.kcl.ac.uk/~shaww/web_page/papers/NormalQuantile1.pdf.
|
|
|
|
مخاطر خفية لمكون شائع في مشروبات الطاقة والمكملات الغذائية
|
|
|
|
|
|
|
"آبل" تشغّل نظامها الجديد للذكاء الاصطناعي على أجهزتها
|
|
|
|
|
|
|
المجمع العلميّ يُواصل عقد جلسات تعليميّة في فنون الإقراء لطلبة العلوم الدينيّة في النجف الأشرف
|
|
|
