


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 1-12-2020
Date: 17-9-2020
Date: 30-11-2019
|
Gelfond's theorem, also called the Gelfond-Schneider theorem, states that 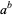 is transcendental if
is transcendental if
1. 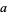 is algebraic
is algebraic 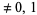 and
and
2. 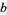 is algebraic and irrational.
is algebraic and irrational.
This provides a partial solution to the seventh of Hilbert's problems. It was proved independently by Gelfond (1934ab) and Schneider (1934ab).
This establishes the transcendence of Gelfond's constant 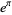 (since
(since 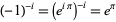 ) and the Gelfond-Schneider constant
) and the Gelfond-Schneider constant 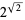 .
.
Gelfond's theorem is implied by Schanuel's conjecture (Chow 1999).
REFERENCES:
Baker, A. Transcendental Number Theory. London: Cambridge University Press, 1990.
Borwein, J. and Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, pp. 82-83, 2003.
Chow, T. Y. "What is a Closed-Form Number?" Amer. Math. Monthly 106, 440-448, 1999.
Courant, R. and Robbins, H. What Is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed. Oxford, England: Oxford University Press, p. 107, 1996.
Gelfond, A. O. "Sur le septième Problème de D. Hilbert." Comptes Rendus Acad. Sci. URSS Moscou 2, 1-6, 1934a.
Gelfond, A. O. "Sur le septième Problème de Hilbert." Bull. Acad. Sci. URSS Leningrade 7, 623-634, 1934b.
Schneider, T. "Transzendenzuntersuchungen periodischer Funktionen. I." J. reine angew. Math. 172, 65-69, 1934a.
Schneider, T. "Transzendenzuntersuchungen periodischer Funktionen. II." J. reine angew. Math. 172, 70-74, 1934b.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|