المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Figurate Number Triangle |
 575
 05:13 مساءً
date: 12-12-2020 |
Author : Smith, D. E 
Book or Source : A Source Book in Mathematics. New York: Dover 
Page and Part : p. 86|
Read More
Date: 13-1-2021
738
Date: 30-1-2020
1033
Date: 27-1-2020
626
|
A Pascal's triangle written in a square grid and padded with zeros, as written by Jakob Bernoulli (Smith 1984). The figurate number triangle therefore has entries
 |
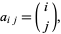(1) |
where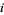 
is the row number, 
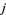the column number, and 
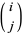a binomial coefficient. Written out explicitly (beginning each row with 
),
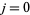![[1 0 0 0 0 0 0 ...; 1 1 0 0 0 0 0 ...; 1 2 1 0 0 0 0 ...; 1 3 3 1 0 0 0 ...; 1 4 6 4 1 0 0 ...; 1 5 10 10 5 1 0 ...; 1 6 15 20 15 6 1 ...; 1 7 21 35 35 21 7 ...; | | | | | | | ...]](https://mathworld.wolfram.com/images/equations/FigurateNumberTriangle/NumberedEquation2.gif) |
(2) |
Then we have the sum identities
 |
 |
 |
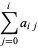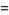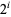(3) |
 |
 |
 |
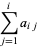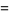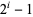(4) |
 |
 |
 |
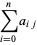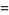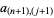(5) |
 |
 |
 |
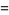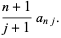(6) |
REFERENCES:
Smith, D. E. A Source Book in Mathematics. New York: Dover, p. 86, 1984.
|
|
|
|
مخاطر خفية لمكون شائع في مشروبات الطاقة والمكملات الغذائية
|
|
|
|
|
|
|
"آبل" تشغّل نظامها الجديد للذكاء الاصطناعي على أجهزتها
|
|
|
|
|
|
|
تستخدم لأول مرة... مستشفى الإمام زين العابدين (ع) التابع للعتبة الحسينية يعتمد تقنيات حديثة في تثبيت الكسور المعقدة
|
|
|
