
Arm Contortions
 المؤلف:
Franklin Potter and Christopher Jargodzki
المؤلف:
Franklin Potter and Christopher Jargodzki
 المصدر:
Mad about Modern Physics
المصدر:
Mad about Modern Physics
 الجزء والصفحة:
p 25
الجزء والصفحة:
p 25
 7-10-2016
7-10-2016
 532
532
Arm Contortions
Normally, the rotation of an object about a fixed axis by 360 degrees brings the object back to its initial orientation. However, Barbara has the agility to do the following double rotation. She places a small object or book in her right hand, holding the object horizontal and noting its orientation in the room. While imagining a vertical axis from floor to ceiling, the book is moved inward first and then under the upper arm, keeping the book horizontal and rotating the object completely around this vertical axis back to its initial position. Her arm is now twisted. Can she untwist by rotating her arm a second time in the same direction?
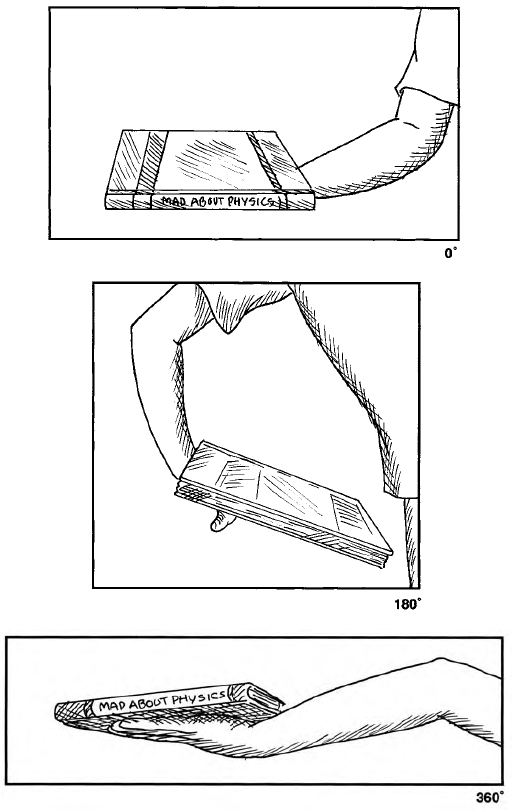
Answer
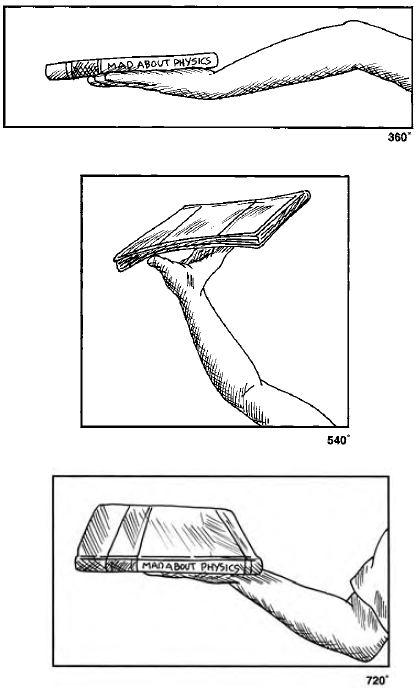
Yes, if one allows the arm to move overhead. This second rotation untwists the arm and brings the orientation of the book back to the initial one again. One can say that the arm-object pair requires two 360-degree rotations to return to the initial orientation. Such an entity is said to mathematically correspond to a spin 1⁄2 system that is, related to the continuous symmetry group SU(2). Any lepton or quark wave function, such as the electron wave function, behaves in this way with respect to rotations and angular momentum.
Spheres, cubes, and other objects with spatial symmetry also can be classified as spin 1⁄2 that is, their rotations are described by symmetry groups that are subgroups of SU(2) and SU′ (2) = SU(2) × Ci, where Ci is the two-element inversion group. For the Platonic solids, the rotational symmetry groups are discrete instead of being continuous, and some of these symmetry groups are subgroups of both SU(2) and SU′ (2) because among all the elements of both can be found the elements of finite order for the discrete subgroups.
As you know, our practical experience is mostly with spin 1 entities that is, those needing a 360-degree rotation to return to the initial orientation. Mathematically, these spin 1 properties can be constructed from the spin 1⁄2 symmetry properties. Mathematicians know that even more fundamental are the reflection groups from which all spin 1⁄2 properties can be derived as two reflections in perpendicular planes. The two books listed below discuss these hierarchical relationships and many more.
 الاكثر قراءة في طرائف الفيزياء
الاكثر قراءة في طرائف الفيزياء
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


