Harmonic Divisor Number

A number 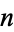 for which the harmonic mean of the divisors of 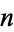, i.e., 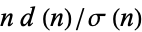, is an integer, where  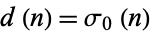is the number of positive integer divisors of  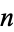and 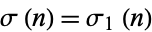 is the divisor function. For example, the divisors of  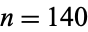are 1, 2, 4, 5, 7, 10, 14, 20, 28, 35, 70, and 140, giving

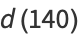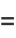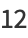			(1)
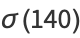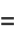			(2)
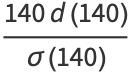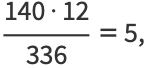			(3)

so 140 is a harmonic divisor number. Harmonic divisor numbers are also called Ore numbers. Garcia (1954) gives the 45 harmonic divisor numbers less than 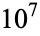. The first few are 1, 6, 28, 140, 270, 496, ... (OEIS A001599).

For distinct primes 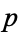 and 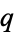, harmonic divisor numbers are equivalent to even perfect numbers for numbers of the form 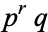. Mills (1972) proved that if there exists an odd positive harmonic divisor number 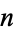, then  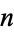has a prime-power factor greater than .

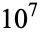Another type of number called "harmonic" is the harmonic number.

REFERENCES:

Edgar, H. M. W. "Harmonic Numbers." Amer. Math. Monthly 99, 783-789, 1992.

Garcia, M. "On Numbers with Integral Harmonic Mean." Amer. Math. Monthly 61, 89-96, 1954.

Guy, R. K. "Almost Perfect, Quasi-Perfect, Pseudoperfect, Harmonic, Weird, Multiperfect and Hyperperfect Numbers." §B2 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 45-53, 1994.

Mills, W. H. "On a Conjecture of Ore." Proceedings of the 1972 Number Theory Conference. University of Colorado, Boulder, pp. 142-146, 1972.

Ore, Ø. "On the Averages of the Divisors of a Number." Amer. Math. Monthly 55, 615-619, 1948.

Pomerance, C. "On a Problem of Ore: Harmonic Numbers." Unpublished manuscript, 1973.

Sloane, N. J. A. Sequence A001599/M4185 in "The On-Line Encyclopedia of Integer Sequences."

Sloane, N. J. A. and Plouffe, S. Figure M4299 in The Encyclopedia of Integer Sequences. San Diego: Academic Press, 1995.

Zachariou, A. and Zachariou, E. "Perfect, Semi-Perfect and Ore Numbers." Bull. Soc. Math. Gréce (New Ser.) 13, 12-22, 1972.