


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 23-1-2021
Date: 25-11-2020
Date: 8-7-2020
|
Define the abundancy 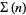 of a positive integer
of a positive integer 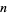 as
as
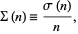 |
(1) |
where 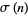 is the divisor function. Then a pair of distinct numbers
is the divisor function. Then a pair of distinct numbers 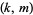 is a friendly pair (and
is a friendly pair (and 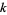 is said to be a friend of
is said to be a friend of 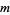 ) if their abundancies are equal:
) if their abundancies are equal:
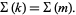 |
(2) |
For example, (4320, 4680) is a friendly pair since 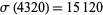 ,
, 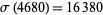 , and
, and
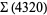 |
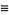 |
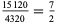 |
(3) |
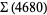 |
 |
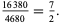 |
(4) |
Another example is 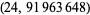 , which has index 5/2. The first few friendly pairs, ordered by smallest maximum element are (6, 28), (30, 140), (80, 200), (40, 224), (12, 234), (84, 270), (66, 308), ... (OEIS A050972 and A050973).
, which has index 5/2. The first few friendly pairs, ordered by smallest maximum element are (6, 28), (30, 140), (80, 200), (40, 224), (12, 234), (84, 270), (66, 308), ... (OEIS A050972 and A050973).
Friendly triples and higher-order tuples are also possible. Friendly triples include (2160, 5400, 13104), (9360, 21600, 23400), and (4320, 4680, 26208), friendly quadruples include (6, 28, 496, 8128), (3612, 11610, 63984, 70434), (3948, 12690, 69936, 76986), and friendly quintuples include (84, 270, 1488, 1638, 24384), (30, 140, 2480, 6200, 40640), (420, 7440, 8190, 18600, 121920).
Numbers that have friends are called friendly numbers, and numbers that do not have friends are called solitary numbers. A sufficient (but not necessary) condition for 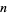 to be a solitary number is that
to be a solitary number is that 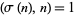 , where
, where 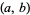 is the greatest common divisor of
is the greatest common divisor of 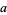 and
and 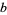 . There are some numbers that can easily be proved to be solitary, but the status of numbers 10, 14, 15, 20, and many others remains unknown (Hickerson 2002).
. There are some numbers that can easily be proved to be solitary, but the status of numbers 10, 14, 15, 20, and many others remains unknown (Hickerson 2002).
Hoffman (1998, p. 45) uses the term "friendly numbers" to describe amicable pairs.
REFERENCES:
Anderson, C. W. and Hickerson, D. Problem 6020. "Friendly Integers." Amer. Math. Monthly 84, 65-66, 1977.
Hickerson, D. "Re: friendly/solitary numbers [was: typos]" seqfan@ext.jussieu.fr mailing list. 19 Sep 2002.
Hoffman, P. The Man Who Loved Only Numbers: The Story of Paul Erdős and the Search for Mathematical Truth. New York: Hyperion, 1998.
Pollack, P. and Pomerance, C. "Some Problems of Erdős on the Sum-of-Divisors Function." Trans. Amer. Math. Soc. 3, 1-26, 2016.
Sloane, N. J. A. Sequences A050972 and A050973 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|