Fermat's Divisor Problem

In 1657, Fermat posed the problem of finding solutions to

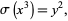and solutions to

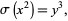where 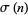 is the divisor function (Dickson 2005).

The first few solutions to 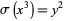 are 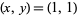, (7, 20), (751530, 1292054400) (OEIS A008849 and A048948) .... Lucas stated that there are an infinite number of solutions (Dickson 2005, p. 56), but only solutions up to the fourth are known to be complete.

The first few solutions to 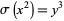 are 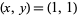, (43098, 1729), ... (OEIS A008850 and A048949), with only solutions up to the second known to be complete.

REFERENCES:

Beiler, A. H. Recreations in the Theory of Numbers: The Queen of Mathematics Entertains. New York: Dover, p. 9, 1966.

Dickson, L. E. History of the Theory of Numbers, Vol. 1: Divisibility and Primality. New York: Dover, pp. 54-58, 2005.

Sloane, N. J. A. Sequences A008849, A008850, A048948, and A048949 in "The On-Line Encyclopedia of Integer Sequences."