


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 30-7-2020
Date: 3-3-2020
Date: 13-1-2020
|
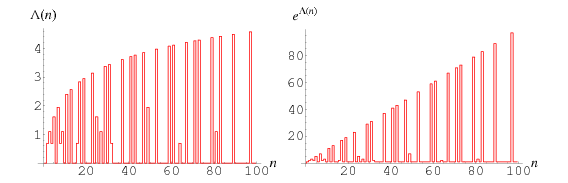
The Mangoldt function is the function defined by
 |
(1) |
sometimes also called the lambda function. 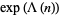 has the explicit representation
has the explicit representation
 |
(2) |
where 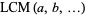 denotes the least common multiple. The first few values of
denotes the least common multiple. The first few values of 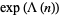 for
for 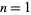 , 2, ..., plotted above, are 1, 2, 3, 2, 5, 1, 7, 2, ... (OEIS A014963).
, 2, ..., plotted above, are 1, 2, 3, 2, 5, 1, 7, 2, ... (OEIS A014963).
The Mangoldt function is implemented in the Wolfram Language as MangoldtLambda[n].
It satisfies the divisor sums
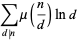 |
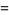 |
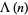 |
(3) |
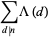 |
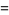 |
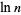 |
(4) |
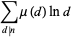 |
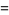 |
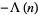 |
(5) |
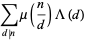 |
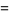 |
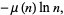 |
(6) |
where 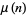 is the Möbius function (Hardy and Wright 1979, p. 254).
is the Möbius function (Hardy and Wright 1979, p. 254).
The Mangoldt function is related to the Riemann zeta function  by
by
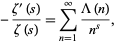 |
(7) |
where ![R[s]>1](https://mathworld.wolfram.com/images/equations/MangoldtFunction/Inline19.gif) (Hardy 1999, p. 28; Krantz 1999, p. 161; Edwards 2001, p. 50).
(Hardy 1999, p. 28; Krantz 1999, p. 161; Edwards 2001, p. 50).
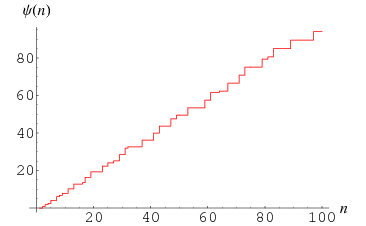
The summatory Mangoldt function, illustrated above, is defined by
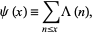 |
(8) |
where 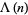 is the Mangoldt function, and is also known as the second Chebyshev function (Edwards 2001, p. 51).
is the Mangoldt function, and is also known as the second Chebyshev function (Edwards 2001, p. 51). 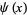 is given by the so-called explicit formula
is given by the so-called explicit formula
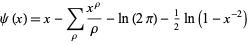 |
(9) |
for 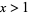 and
and  not a prime or prime power (Edwards 2001, pp. 49, 51, and 53), and the sum is over all nontrivial zeros
not a prime or prime power (Edwards 2001, pp. 49, 51, and 53), and the sum is over all nontrivial zeros 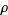 of the Riemann zeta function
of the Riemann zeta function 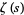 , i.e., those in the critical strip so
, i.e., those in the critical strip so ![0<R[rho]<1](https://mathworld.wolfram.com/images/equations/MangoldtFunction/Inline26.gif) (Montgomery 2001), and interpreted as
(Montgomery 2001), and interpreted as
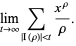 |
(10) |
Vallée Poussin's version of the prime number theorem states that
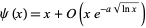 |
(11) |
for some 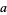 (Davenport 1980, Vardi 1991). The prime number theorem is equivalent to the statement that
(Davenport 1980, Vardi 1991). The prime number theorem is equivalent to the statement that
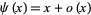 |
(12) |
as 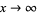 (Dusart 1999).
(Dusart 1999).
Von Mangoldt proved his formula 30 years after Riemann's paper, which contained a related formula that inspired von Mangoldt's. Von Mangoldt's formula was then used to prove the prime number theorem in the equivalent form
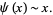 |
(13) |
The Riemann hypothesis is equivalent to
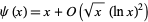 |
(14) |
(Davenport 1980, p. 114; Vardi 1991).
Vardi (1991, p. 155) also gives the interesting formula
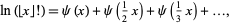 |
(15) |
where 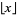 is the floor function and
is the floor function and 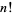 is a factorial.
is a factorial.
REFERENCES:
Costa Pereira, N. "Estimates for the Chebyshev Function 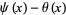 ." Math. Comput. 44, 211-221, 1985.
." Math. Comput. 44, 211-221, 1985.
Costa Pereira, N. "Corrigendum: Estimates for the Chebyshev Function 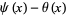 ." Math. Comput. 48, 447, 1987.
." Math. Comput. 48, 447, 1987.
Costa Pereira, N. "Elementary Estimates for the Chebyshev Function 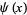 and for the Möbius Function
and for the Möbius Function 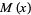 ." Acta Arith. 52, 307-337, 1989.
." Acta Arith. 52, 307-337, 1989.
Davenport, H. Multiplicative Number Theory, 2nd ed. New York: Springer-Verlag, p. 104, 1980.
Dusart, P. "Inégalités explicites pour 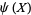 ,
, 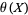 ,
, 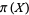 et les nombres premiers." C. R. Math. Rep. Acad. Sci. Canad 21, 53-59, 1999.
et les nombres premiers." C. R. Math. Rep. Acad. Sci. Canad 21, 53-59, 1999.
Edwards, H. M. "Derivation of von Mangoldt's Formula for 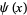 ." §3.2 in Riemann's Zeta Function. New York: Dover, pp. 50-54, 2001.
." §3.2 in Riemann's Zeta Function. New York: Dover, pp. 50-54, 2001.
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, p. 28, 1999.
Hardy, G. H. and Wright, E. M. An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, 1979.
Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, p. 109, 2003.
Krantz, S. G. "The Lambda Function" and "Relation of the Zeta Function to the Lambda Function." §13.2.10 and 13.2.11 in Handbook of Complex Variables. Boston, MA: Birkhäuser, p. 161, 1999.
Montgomery, H. L. "Harmonic Analysis as Found in Analytic Number Theory." In Twentieth Century Harmonic Analysis--A Celebration. Proceedings of the NATO Advanced Study Institute Held in Il Ciocco, July 2-15, 2000 (Ed. J. S. Byrnes). Dordrecht, Netherlands: Kluwer, pp. 271-293, 2001.
Rosser, J. B. and Schoenfeld, L. "Sharper Bounds for Chebyshev Functions 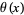 and
and 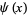 ." Math. Comput. 29, 243-269, 1975.
." Math. Comput. 29, 243-269, 1975.
Schoenfeld, L. "Sharper Bounds for Chebyshev Functions 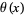 and
and 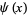 . II." Math. Comput. 30, 337-360, 1976.
. II." Math. Comput. 30, 337-360, 1976.
Sloane, N. J. A. Sequence A014963 in "The On-Line Encyclopedia of Integer Sequences."
Vardi, I. Computational Recreations in Mathematica. Reading, MA: Addison-Wesley, pp. 146-147, 152-153, and 249, 1991.



|
|
|
|
"عادة ليلية" قد تكون المفتاح للوقاية من الخرف
|
|
|
|
|
|
|
ممتص الصدمات: طريقة عمله وأهميته وأبرز علامات تلفه
|
|
|
|
|
|
|
المجمع العلمي للقرآن الكريم يقيم جلسة حوارية لطلبة جامعة الكوفة
|
|
|