


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 21-10-2020
Date: 14-10-2020
Date: 18-12-2019
|
An integer 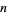 is
is 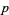 -balanced for
-balanced for 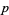 a prime if, among all nonzero binomial coefficients
a prime if, among all nonzero binomial coefficients 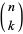 for
for 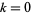 , ...,
, ..., 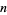 (mod
(mod 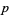 ), there are equal numbers of quadratic residues and nonresidues (mod
), there are equal numbers of quadratic residues and nonresidues (mod 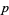 ). Let
). Let 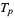 be the set of integers
be the set of integers 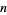 ,
, 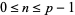 , that are
, that are 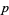 -balanced. Among all the primes
-balanced. Among all the primes 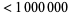 , only those with
, only those with 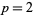 , 3, and 11 have
, 3, and 11 have 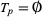 .
.
The following table gives the 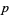 -balanced integers for small primes
-balanced integers for small primes 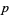 (OEIS A093755).
(OEIS A093755).
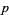 |
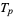 |
| 2 | 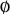 |
| 3 | 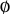 |
| 5 | 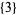 |
| 7 | 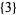 |
| 11 | 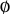 |
| 13 | 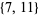 |
| 17 | 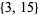 |
REFERENCES:
Garfield, R. and Wilf, H. S. "The Distribution of the Binomial Coefficients Modulo 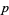 ." J. Number Th. 41, 1-5, 1992.
." J. Number Th. 41, 1-5, 1992.
Sloane, N. J. A. Sequence A093755 in "The On-Line Encyclopedia of Integer Sequences."
Wilf, H. "On Crossing Numbers, and Some Unsolved Problems." In Combinatorics, Geometry, and Probability: A Tribute to Paul Erdős. Papers from the Conference in Honor of Erdős' 80th Birthday Held at Trinity College, Cambridge, March 1993 (Ed. B. Bollobás and A. Thomason). Cambridge, England: Cambridge University Press, pp. 557-562, 1997.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|