Sierpiński's Composite Number Theorem

As proved by Sierpiński (1960), there exist infinitely many positive odd numbers 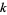 such that  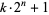is composite for every 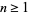. Numbers  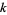with this property are called Sierpiński numbers of the second kind, and analogous numbers with the plus sign replaced by a minus are called Riesel numbers. It is conjectured that the smallest value of  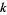for a Sierpiński number of the second kind is  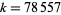(although a handful of smaller candidates remain to be eliminated) and that the smallest Riesel number is .

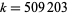REFERENCES:

Ballinger, R. "The Riesel Problem: Definition and Status." https://www.prothsearch.net/rieselprob.html.

Ballinger, R. "The Sierpinski Problem: Definition and Status." https://www.prothsearch.net/sierp.html.

Ballinger, R. and Keller, W. "The Riesel Problem: Search for Remaining Candidates." https://www.prothsearch.net/rieselsearch.html.

Buell, D. A. and Young, J. "Some Large Primes and the Sierpiński Problem." SRC Tech. Rep. 88004, Supercomputing Research Center, Lanham, MD, 1988.

Helm, L. and Norris, D. "Seventeen or Bust: A Distributed Attack on the Sierpinski Problem." https://www.seventeenorbust.com/.

Jaeschke, G. "On the Smallest  such that 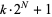 are Composite." Math. Comput. 40, 381-384, 1983.

Jaeschke, G. Corrigendum to "On the Smallest 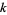 such that  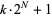are Composite." Math. Comput. 45, 637, 1985.

Keller, W. "Factors of Fermat Numbers and Large Primes of the Form 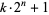." Math. Comput. 41, 661-673, 1983.

Keller, W. "Factors of Fermat Numbers and Large Primes of the Form 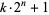, II." Preprint available at https://www.rrz.uni-hamburg.de/RRZ/W.Keller/.

Ribenboim, P. The New Book of Prime Number Records. New York: Springer-Verlag, pp. 357-359, 1996.

Riesel, H. "Några stora primtal." Elementa 39, 258-260, 1956.

Sierpiński, W. "Sur un problème concernant les nombres 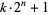." Elem. d. Math. 15, 73-74, 1960.