


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 30-1-2021
Date: 25-8-2020
Date: 28-10-2019
|
The constant 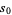 in Schnirelmann's theorem such that every integer
in Schnirelmann's theorem such that every integer 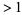 is a sum of at most
is a sum of at most 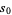 primes. Of course, by Vinogradov's theorem, it is known that 4 primes suffice for all sufficiently large numbers, but this constant gives a sufficient number for all numbers. The best current estimate is
primes. Of course, by Vinogradov's theorem, it is known that 4 primes suffice for all sufficiently large numbers, but this constant gives a sufficient number for all numbers. The best current estimate is 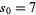 (Ramaré 1995), and a summary of progress on upper bounds for
(Ramaré 1995), and a summary of progress on upper bounds for 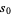 is summarized in the following table.
is summarized in the following table.
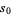 |
author |
| 7 | Ramaré (1995) |
| 19 | Riesel and Vaughan (1983) |
| 26 | Deshouillers (1977) |
| 27 | Vaughan (1977) |
| 55 | Klimov (1975) |
| 115 | Klimov et al. (1972) |
| 159 | Deshouillers (1973) |
REFERENCES:
Deshouillers, J.-M. No. 17 in "Amélioration de la constante de Šnirelman dans le probléme de Goldbach." Séminaire Delange-Pisot-Poitou (14e année: 1972/73). Théorie des nombres: Fascicule 2: Exposés 17 à 26, et Groupe d'étude. Paris: Secrétariat Mathématique, pp. 1-4, 1973.
Deshouillers, J.-M. "Sur la constante de Šnirel'man." No. G16 in Séminaire Delange-Pisot-Poitou, 17e année (1975/76). Théorie des nombres: Fascicule 2: Exposés 23 à 31 et Groupe d'étude. Paris: Secrétariat Math., pp. 1-6, 1977.
Klimov, K. I. Naucn. Trudy Kuibysev Gos. Ped. Inst. 158, 14-30, 1975.
Klimov, N. I.; Pil'tjaĭ, G. Z.; and Šeptickaja, T. A. "An Estimate of the Absolute Constant in the Goldbach-Šnirel'man Problem." In Issledovaniya po teorii chisel, Vyp. 4. [Studies in number theory, No. 4] (Ed. N. Lenskoĭ). Saratov: Izdat. Saratov. Univ., pp. 35-51, 1972.
Ramaré, O. "On Šnirel'man's Constant." Ann. Scuola Norm. Sup. Pisa Cl. Sci. 22, 645-706, 1995.
Riesel, H. and Vaughan, R. C. "On Sums of Primes." Ark. Mat. 21, 46-74, 1983.
Vaughan, R. C. "On the Estimation of Schnirelman's Constant." J. reine angew. Math. 290, 93-108, 1977.



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
المجمع العلمي ينظّم ندوة حوارية حول مفهوم العولمة الرقمية في بابل
|
|
|