


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 5-6-2020
Date: 5-8-2020
Date: 12-5-2020
|
The 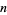 th Smarandache-Wellin number is formed from the consecutive number sequence obtained by concatenating of the digits of the first
th Smarandache-Wellin number is formed from the consecutive number sequence obtained by concatenating of the digits of the first 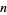 primes. The first few are 2, 23, 235, 2357, 235711, ... (OEIS A019518; Smith 1996, Mudge 1997). This sequence converges to the digits of the Copeland-Erdős constant.
primes. The first few are 2, 23, 235, 2357, 235711, ... (OEIS A019518; Smith 1996, Mudge 1997). This sequence converges to the digits of the Copeland-Erdős constant.
Prime Smarandache-Wellin numbers are called Smarandache-Wellin primes.
REFERENCES:
Crandall, R. and Pomerance, C. Prime Numbers: A Computational Perspective, 2nd ed. New York: Springer-Verlag, 2005.
Ibstedt, H. "Smarandache Concatenated Sequences." Ch. 5 in Computer Analysis of Number Sequences. Lupton, AZ: American Research Press, pp. 75-79, 1998.
Mudge, M. "Not Numerology but Numeralogy!" Personal Computer World, 279-280, 1997.
Sloane, N. J. A. Sequence A019518 in "The On-Line Encyclopedia of Integer Sequences."
Smith, S. "A Set of Conjectures on Smarandache Sequences." Bull. Pure Appl. Sci. 15E, 101-107, 1996.



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|