


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 12-7-2020
Date: 26-6-2020
Date: 16-8-2020
|
The Feit-Thompson conjecture asserts that there are no primes 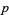 and
and 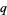 for which
for which 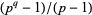 and
and 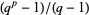 have a common factor.
have a common factor.
Parker noticed that if this were true, it would greatly simplify the lengthy proof of the Feit-Thompson theorem that every group of odd order is solvable. (Guy 1994, p. 81). However, the counterexample (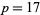 ,
, 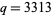 ) with a common factor
) with a common factor 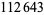 was subsequently found by Stephens (1971), demonstrating that the conjecture is, in fact, false.
was subsequently found by Stephens (1971), demonstrating that the conjecture is, in fact, false.
No other such pairs exist with both values less than 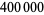 .
.
REFERENCES:
Apostol, T. M. "The Resultant of the Cyclotomic Polynomials 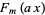 and
and 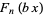 ." Math. Comput. 29, 1-6, 1975.
." Math. Comput. 29, 1-6, 1975.
Feit, W. and Thompson, J. G. "A Solvability Criterion for Finite Groups and Some Consequences." Proc. Nat. Acad. Sci. USA 48, 968-970, 1962.
Feit, W. and Thompson, J. G. "Solvability of Groups of Odd Order." Pacific J. Math. 13, 775-1029, 1963.
Guy, R. K. Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, p. 81, 1994.
Stephens, N. M. "On the Feit-Thompson Conjecture." Math. Comput. 25, 625, 1971.
Wells, D. G. The Penguin Dictionary of Curious and Interesting Numbers. London: Penguin, p. 17, 1986.



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|