


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 9-6-2020
Date: 12-12-2020
Date: 7-8-2020
|
The Thue-Morse constant, also called the parity constant, is given by the concatenated digits of the Thue-Morse sequence
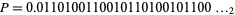 |
(1) |
(OEIS A010060) interpreted as a binary number. In, decimal, it can be written as
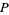 |
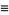 |
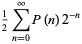 |
(2) |
 |
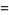 |
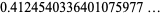 |
(3) |
(OEIS A014571), where 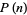 is the parity of
is the parity of 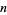 (i.e., the numbers of 1s in the binary representation of
(i.e., the numbers of 1s in the binary representation of 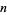 , computed modulo 2).
, computed modulo 2).
Dekking (1977) proved that the Thue-Morse constant is transcendental, and Allouche and Shallit give a complete proof correcting a minor error of Dekking.
The Thue-Morse constant can be written in base 2 by stages by taking the previous iteration 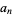 , taking the complement
, taking the complement 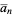 obtained by reversing the digits of
obtained by reversing the digits of 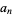 , and appending, producing
, and appending, producing
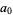 |
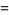 |
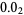 |
(4) |
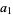 |
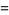 |
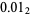 |
(5) |
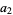 |
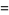 |
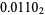 |
(6) |
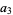 |
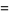 |
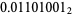 |
(7) |
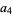 |
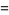 |
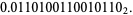 |
(8) |
This can be written symbolically as
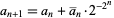 |
(9) |
with 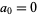 . Here, the complement is the number
. Here, the complement is the number 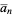 such that
such that 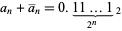 , which can be found from
, which can be found from
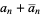 |
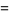 |
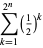 |
(10) |
 |
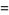 |
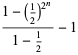 |
(11) |
 |
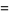 |
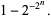 |
(12) |
Therefore,
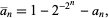 |
(13) |
and
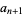 |
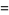 |
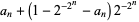 |
(14) |
 |
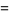 |
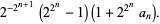 |
(15) |
The first few iterations give 0, 1/4, 3/8, 105/256, 13515/32768, ... (OEIS A074072 and A074073).
The regular continued fraction for the Thue-Morse constant is [0 2 2 2 1 4 3 5 2 1 4 2 1 5 44 1 4 1 2 4 1 1 1 5 14 1 50 15 5 1 1 1 4 2 1 4 1 43 1 4 1 2 1 3 16 1 2 1 2 1 50 1 2 424 1 2 5 2 1 1 1 5 5 2 22 5 1 1 1 1274 3 5 2 1 1 1 4 1 1 15 154 7 2 1 2 2 1 2 1 1 50 1 4 1 2 867374 1 1 1 5 5 1 1 6 1 2 7 2 1650 23 3 1 1 1 2 5 3 84 1 1 1 1284 ...] (OEIS A014572), and seems to continue with sporadic large terms in suspicious-looking patterns. A nonregular continued fraction is
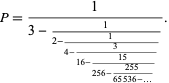 |
(16) |
A related infinite product is
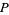 |
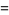 |
![1/4[2-product_(n=0)^(infty)(2^(2^n)-1)/(2^(2^n))]](https://mathworld.wolfram.com/images/equations/Thue-MorseConstant/Inline48.gif) |
(17) |
 |
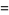 |
![1/4[2-product_(n=0)^(infty)2^(-2^n)(2^(2^n)-1)]](https://mathworld.wolfram.com/images/equations/Thue-MorseConstant/Inline51.gif) |
(18) |
 |
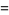 |
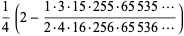 |
(19) |
(Finch 2003, p. 437).
REFERENCES:
Allouche, J. P.; Arnold, A.; Berstel, J.; Brlek, S.; Jockusch, W.; Plouffe, S.; and Sagan, B. "A Relative of the Thue-Morse Sequence." Discr. Math. 139, 455-461, 1995.
Allouche, J. P. and Shallit, J. "The Ubiquitous Prouhet-Thue-Morse Sequence." https://www.math.uwaterloo.ca/~shallit/Papers/ubiq.ps.
Dekking, F. M. "Transcendence du nombre de Thue-Morse." Comptes Rendus de l'Academie des Sciences de Paris 285, 157-160, 1977.
Finch, S. R. "Prouhet-Thue-Morse Constant." §6.8 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 436-441, 2003.
Goldstein, S.; Kelly, K. A.; and Speer, E. R. "The Fractal Structure of Rarefied Sums of the Thue-Morse Sequence." J. Number Th. 42, 1-19, 1992.
Schroeppel, R. and Gosper, R. W. Item 122 in Beeler, M.; Gosper, R. W.; and Schroeppel, R. HAKMEM. Cambridge, MA: MIT Artificial Intelligence Laboratory, Memo AIM-239, pp. 56-57, Feb. 1972. https://www.inwap.com/pdp10/hbaker/hakmem/series.html#item122.
Sloane, N. J. A. Sequences A010060, A014571, A014572, A074072, and A074073 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
"عادة ليلية" قد تكون المفتاح للوقاية من الخرف
|
|
|
|
|
|
|
ممتص الصدمات: طريقة عمله وأهميته وأبرز علامات تلفه
|
|
|
|
|
|
|
ضمن أسبوع الإرشاد النفسي.. جامعة العميد تُقيم أنشطةً ثقافية وتطويرية لطلبتها
|
|
|