Cubic Number

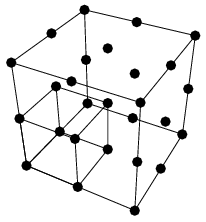
A cubic number is a figurate number of the form 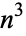 with 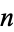 a positive integer. The first few are 1, 8, 27, 64, 125, 216, 343, ... (OEIS A000578). The protagonist Christopher in the novel The Curious Incident of the Dog in the Night-Time recites the cubic numbers to calm himself and prevent himself from wanting to hit someone (Haddon 2003, p. 213).

The generating function giving the cubic numbers is

(1)

The hex pyramidal numbers are equivalent to the cubic numbers (Conway and Guy 1996).

The plots above show the first 255 (top figure) and 511 (bottom figure) cubic numbers represented in binary.

Pollock (1843-1850) conjectured that every number is the sum of at most 9 cubic numbers (Dickson 2005, p. 23). As a part of the study of Waring's problem, it is known that every positive integer is a sum of no more than 9 positive cubes (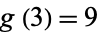, proved by Dickson, Pillai, and Niven in the early twentieth century), that every "sufficiently large" integer is a sum of no more than 7 positive cubes (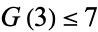). However, it is not known if 7 can be reduced (Wells 1986, p. 70). The number of positive cubes needed to represent the numbers 1, 2, 3, ... are 1, 2, 3, 4, 5, 6, 7, 1, 2, 3, 4, 5, 6, 7, 8, 2, ...(OEIS A002376), and the number of distinct ways to represent the numbers 1, 2, 3, ... in terms of positive cubes are 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 3, 3, 3, 3, 3, 3, 3, 3, 4, 4, 4, 5, 5, 5, 5, ... (OEIS A003108).

In 1939, Dickson proved that the only integers requiring nine positive cubes are 23 and 239. Wieferich proved that only 15 integers require eight cubes: 15, 22, 50, 114, 167, 175, 186, 212, 231, 238, 303, 364, 420, 428, and 454 (OEIS A018889). The quantity 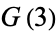 in Waring's problem therefore satisfies 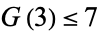, and the largest number known requiring seven cubes is 8042. Deshouillers et al. (2000) conjectured that 7373170279850 is the largest integer that cannot be expressed as the sum of four nonnegative cubes.

The following table gives the first few numbers which require at least 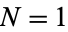, 2, 3, ..., 9 (i.e.,  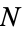or more) positive cubes to represent them as a sum.

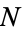	OEIS	numbers
1	A000578	1, 8, 27, 64, 125, 216, 343, 512, ...
2	A003325	2, 9, 16, 28, 35, 54, 65, 72, 91, ...
3	A047702	3, 10, 17, 24, 29, 36, 43, 55, 62, ...
4	A047703	4, 11, 18, 25, 30, 32, 37, 44, 51, ...
5	A047704	5, 12, 19, 26, 31, 33, 38, 40, 45, ...
6	A046040	6, 13, 20, 34, 39, 41, 46, 48, 53, ...
7	A018890	7, 14, 21, 42, 47, 49, 61, 77, ...
8	A018889	15, 22, 50, 114, 167, 175, 186, ...
9	A018888	23, 239

There is a finite set of numbers which cannot be expressed as the sum of distinct positive cubes: 2, 3, 4, 5, 6, 7, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, ...(OEIS A001476).

It is known that every integer is a sum of at most 5 signed cubes (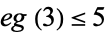 in Waring's problem). It is believed that 5 can be reduced to 4, so that

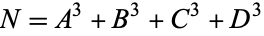(2)

for any number 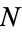, although this has not been proved for numbers of the form 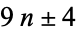. However, every multiple of 6 can be represented as a sum of four signed cubes as a result of the algebraic identity

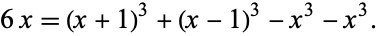(3)

In fact, all numbers 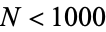 and not of the form  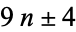are known to be expressible as the sum

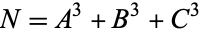(4)

of three (positive or negative) cubes with the exception of 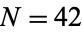, 114, 165, 390, 579, 627, 633, 732, 795, 906, 921, and 975 (Miller and Woollett 1955; Gardiner et al. 1964; Guy 1994, p. 151; Mishima; Elsenhaus and Jahnel 2007; Booker; Huisman 2016). Examples include:

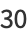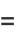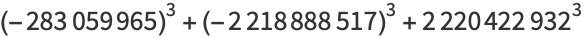			(5)
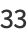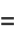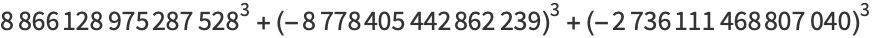			(6)
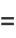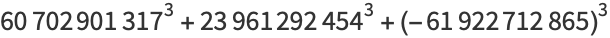			(7)
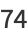			(8)
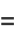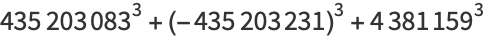			(9)
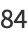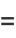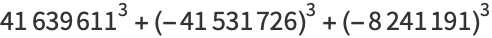			(10)
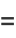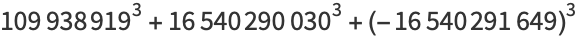			(11)
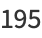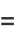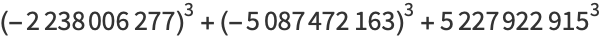			(12)
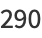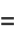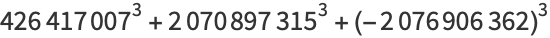			(13)
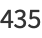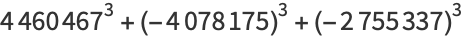			(14)
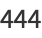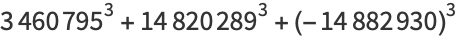			(15)
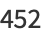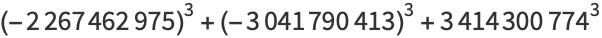			(16)
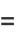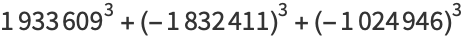			(17)
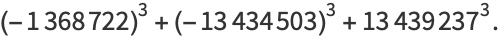			(18)

While it is known that equation (◇) has no solutions for 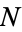 of the form  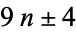(Hardy and Wright 1979, p. 327), there are known reasons for excluding the above integers (Gardiner et al. 1964). Mahler proved that 1 has infinitely many representations as three signed cubes.

If one also excludes numbers of the form 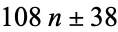, every number can be represented as a sum of four signed cubes, using one of the following algebraic identities, or their complementary identities (via ):

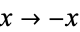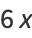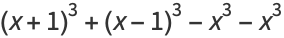			(19)
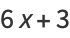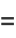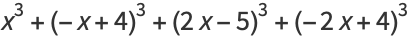			(20)
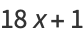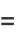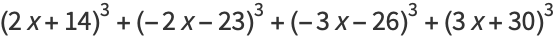			(21)
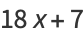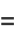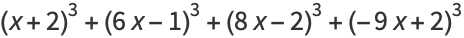			(22)
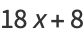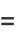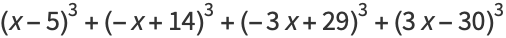			(23)
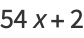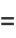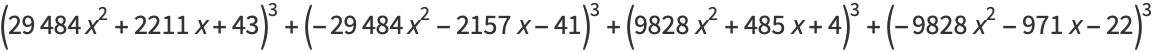			(24)
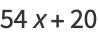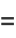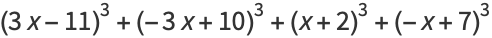			(25)
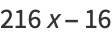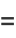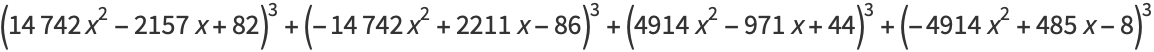			(26)
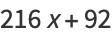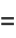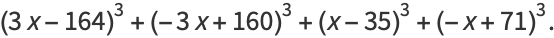			(27)

These identities,and a proof for 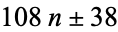 were given by Demjanenko (Demjanenko 1966, Cohen 2004).

The following table gives the numbers which can be represented in exactly 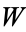 different ways as a sum of  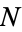positive cubes. (Combining all 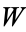s for a given  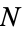then gives the sequences in the previous table.) For example,

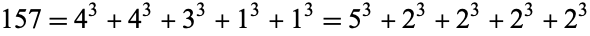(28)

can be represented in 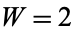 ways by  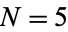cubes. The smallest number representable in  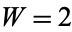ways as a sum of  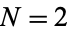cubes,

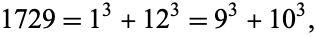(29)

is called the Hardy-Ramanujan number and has special significance in the history of mathematics as a result of a story told by Hardy about Ramanujan. Note that OEIS A001235 is defined as the sequence of numbers which are the sum of cubes in two or more ways, and so appears identical in the first few terms to the 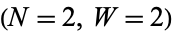 series given below.

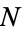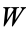		OEIS	numbers
1	0	A007412	2, 3, 4, 5, 6, 7, 9, 10, 11, 12, 13, 14, ...
1	1	A000578	1, 8, 27, 64, 125, 216, 343, 512, ...
2	0	A057903	1, 3, 4, 5, 6, 7, 8, 10, 11, 12, 13, 14, ...
2	1		2, 9, 16, 28, 35, 54, 65, 72, 91, ...
2	2	A018850	1729, 4104, 13832, 20683, 32832, ...
2	3	A003825	87539319, 119824488, 143604279, ...
2	4	A003826	6963472309248, 12625136269928, ...
2	5		48988659276962496, ...
2	6		8230545258248091551205888, ...
3	0	A057904	1, 2, 4, 5, 6, 7, 8, 9, 11, 12, 13, 14, ...
3	1	A025395	3, 10, 17, 24, 29, 36, 43, 55, 62, ...
3	2		251, ...
4	0	A057905	1, 2, 3, 5, 6, 7, 8, 9, 10, 12, 13, 14, ...
4	1	A025403	4, 11, 18, 25, 30, 32, 37, 44, 51, ...
4	2	A025404	219, 252, 259, 278, 315, 376, 467, ...
5	0	A057906	1, 2, 3, 4, 6, 7, 8, 9, 10, 11, 13, 14, 15, ...
5	1	A048926	5, 12, 19, 26, 31, 33, 38, 40, 45, ...
5	2	A048927	157, 220, 227, 246, 253, 260, 267, ...
6	0	A057907	1, 2, 3, 4, 5, 7, 8, 9, 10, 11, 12, 14, 15, ...
6	1	A048929	6, 13, 20, 27, 32, 34, 39, 41, 46, ...
6	2	A048930	158, 165, 184, 221, 228, 235, 247, ...
6	3	A048931	221, 254, 369, 411, 443, 469, 495, ...

The following table gives the possible residues (mod 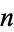) for cubic numbers for  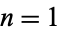to 20, as well as the number of distinct residues .

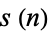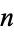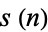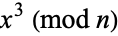2	2	0, 1
3	3	0, 1, 2
4	3	0, 1, 3
5	5	0, 1, 2, 3, 4
6	6	0, 1, 2, 3, 4, 5
7	3	0, 1, 6
8	5	0, 1, 3, 5, 7
9	3	0, 1, 8
10	10	0, 1, 2, 3, 4, 5, 6, 7, 8, 9
11	11	0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
12	9	0, 1, 3, 4, 5, 7, 8, 9, 11
13	5	0, 1, 5, 8, 12
14	6	0, 1, 6, 7, 8, 13
15	15	0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14
16	10	0, 1, 3, 5, 7, 8, 9, 11, 13, 15
17	17	0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16
18	6	0, 1, 8, 9, 10, 17
19	7	0, 1, 7, 8, 11, 12, 18
20	15	0, 1, 3, 4, 5, 7, 8, 9, 11, 12, 13, 15, 16, 17, 19

Dudeney found two rational numbers other than 1 and 2 whose cubes sum to nine,

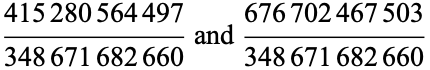(30)

(Gardner 1958). The problem of finding two rational numbers whose cubes sum to six was "proved" impossible by Legendre. However, Dudeney found the simple solutions 17/21 and 37/21.

The only three consecutive integers whose cubes sum to a cube are given by the Diophantine equation

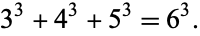(31)

Catalan's conjecture states that 8 and 9 (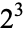 and 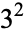) are the only consecutive powers (excluding 0 and 1), i.e., the only solution to Catalan's Diophantine problem. This conjecture has not yet been proved or refuted, although R. Tijdeman has proved that there can be only a finite number of exceptions should the conjecture not hold. It is also known that 8 and 9 are the only consecutive cubic and square numbers (in either order).

There are six positive integers equal to the sum of the digits of their cubes: 1, 8, 17, 18, 26, and 27 (OEIS A046459; Moret Blanc 1879). There are four positive integers equal to the sums of the cubes of their digits:

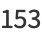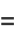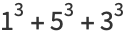			(32)
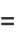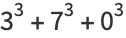			(33)
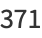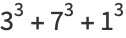			(34)
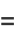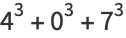			(35)

(Ball and Coxeter 1987). There are two square numbers of the form 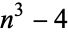:  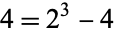and 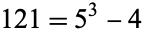 (Le Lionnais 1983). A cube cannot be the concatenation of two cubes, since if  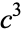is the concatenation of  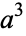and 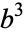, then 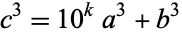, where  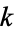is the number of digits in 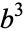. After shifting any powers of 1000 in  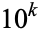into 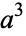, the original problem is equivalent to finding a solution to one of the Diophantine equations

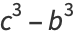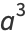			(36)
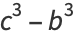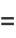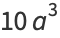			(37)
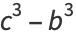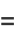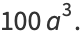			(38)

None of these have solutions in integers, as proved independently by Sylvester, Lucas, and Pepin (Dickson 2005, pp. 572-578).

REFERENCES:

Ball, W. W. R. and Coxeter, H. S. M. Mathematical Recreations and Essays, 13th ed. New York: Dover, p. 14, 1987.

Bertault, F.; Ramaré, O.; and Zimmermann, P. "On Sums of Seven Cubes." Math. Comput. 68, 1303-1310, 1999.

Booker, A. R. "Cracking the Problem with 33." n.d. https://people.maths.bris.ac.uk/~maarb/papers/cubesv1.pdf.

Cohen, H."On Sums of Four Cubes." (Trans. of Demjanenko's paper.) 2004. https://www.math.u-bordeaux.fr/~cohen/.

Conn, B. and Vaserstein, L. "On Sums of Three Integral Cubes." Contemp. Math. 166, 285-294, 1994.

Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, pp. 42-44, 1996.

Davenport, H. "On Waring's Problem for Cubes." Acta Math. 71, 123-143, 1939.

Demjanenko, V. "On Sums of Four Cubes." Izvesti Vischik Outchetsnik Zavedenii Math. 54, 64-69, 1966.

Deshouillers, J.-M.; Hennecart, F.; and Landreau, B. "7 373 170 279 850." Math. Comput. 69, 421-439, 2000.

Dickson, L. E. History of the Theory of Numbers, Vol. 2: Diophantine Analysis. New York: Dover, 2005.

Elkies, N. D. "Rational Points Near Curves and Small Nonzero 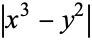 via Lattice Reduction." In Algorithmic Number Theory. Proceedings of the 4th International Symposium (ANTS-IV) held at the Universiteit Leiden, Leiden, July 2-7, 2000 (Ed. W. Bosma). Berlin: Springer-Verlag, pp. 33-63, 2000. https://arxiv.org/abs/math.NT/0005139.

Elsenhaus, A.-S. and Jahnel, J. "List of Solutions of 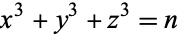 for 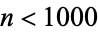 Neither a Cube Nor Twice a Cube." Apr. 19, 2007. https://www.uni-math.gwdg.de/jahnel/Arbeiten/Liste/threecubes_20070419.txt.

Elsenhaus, A.-S. and Jahnel, J. "New Sums of Three Cubes." Math. Comput. 78, 1227-1230, 2009.

Gardiner, V. L.; Lazarus, R. B.; and Stein, P. R. "Solutions of the Diophantine Equation 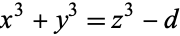." Math. Comput. 18, 408-413, 1964.

Gardner, M. "Mathematical Games: About Henry Ernest Dudeney, A Brilliant Creator of Puzzles." Sci. Amer. 198, 108-112, Jun. 1958.

Guy, R. K. "Sum of Four Cubes." §D5 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 151-152, 1994.

Haddon, M. The Curious Incident of the Dog in the Night-Time. New York: Vintage, 2003.

Hardy, G. H. and Wright, E. M. "Representation by Cubes and Higher Powers." Ch. 21 in An Introduction to the Theory of Numbers, 5th ed. Oxford, England: Clarendon Press, pp. 317-339, 1979.

Heath-Brown, D. R.; Lioen, W. M.; and te Riele, H. J. J. "On Solving the Diophantine Equation 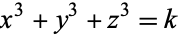 on a Vector Computer." Math. Comput. 61, 235-244, 1993.

Huisman, S. G. "Newer Sums of Three Cubes." 26 Apr 2016. https://arxiv.org/abs/1604.07746.

Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 53, 1983.

Miller, J. C. P. and Woollett, M. F. C. "Solutions of the Diophantine Equation 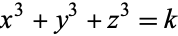." J. London Math. Soc. 30, 101-110, 1955.

Mishima, H. "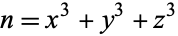." https://www.asahi-net.or.jp/~kc2h-msm/mathland/math04/cube00.htm.

Mishima, H. "The Mathematician's Secret Room." https://www.asahi-net.or.jp/~KC2H-MSM/mathland/math04/cube00.htm.

Pollock, F. "On the Extension of the Principle of Fermat's Theorem of the Polygonal Numbers to the Higher Orders of Series Whose Ultimate Differences Are Constant. With a New Theorem Proposed, Applicable to All the Orders." Abs. Papers Commun. Roy. Soc. London 5, 922-924, 1843-1850.

Sloane, N. J. A. Sequences A000578/M4499, A001235, A001476, A002376/M0466, A003108/M0209, A003072, A003325, A003327, A003328, A003825, A003826, A007412/M0493, A011541, A018850, A018888, A018889, A018890, A025395, A046040, A046041, A046459, A048926, A048927, A048928, A048929, A048930, A048931, A048932, A057903, A057904, A057905, A057906, and A057907 in "The On-Line Encyclopedia of Integer Sequences."

Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, p. 70, 1986.