


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 10-5-2020
Date: 1-9-2020
Date: 16-11-2020
|
The pseudosquare 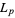 modulo the odd prime
modulo the odd prime 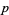 is the least nonsquare positive integer that is congruent to 1 (mod 8) and for which the Legendre symbol
is the least nonsquare positive integer that is congruent to 1 (mod 8) and for which the Legendre symbol 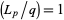 for all odd primes
for all odd primes 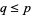 . They were first considered by Kraitchik (1924, pp. 41-46), who computed all up to
. They were first considered by Kraitchik (1924, pp. 41-46), who computed all up to 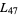 , and were named by Lehmer (1954). Hall (1933) showed that the values of
, and were named by Lehmer (1954). Hall (1933) showed that the values of 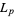 are unbounded as
are unbounded as 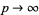 .
.
Pseudosquares arise in primality proving. Lukes et al. (1996) computed pseudosquares up to 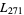 . The first few pseudosquares are 73, 241, 1009, 2641, 8089, ... (OEIS A002189). Note that the pseudosquares need not be unique so, for example,
. The first few pseudosquares are 73, 241, 1009, 2641, 8089, ... (OEIS A002189). Note that the pseudosquares need not be unique so, for example, 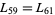 ,
, 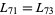 ,
, 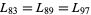 , and so on.
, and so on.
REFERENCES:
Bernstein, D. J. "Doubly Focused Enumeration of Locally Square Polynomial Values." Draft, Dec. 31, 2001. https://cr.yp.to/papers/focus.ps.
Hall, M. "Quadratic Residues in Factorization." Bull. Amer. Math. Soc. 39, 758-763, 1933.
Kraitchik, M. Recherches sue la théorie des nombres. Paris: Gauthier-Villars, 1924.
Lehmer, D. H. "A Sieve Problem on 'Pseudo-Squares.' " Math. Tables Other Aids Comput. 8, 241-242, 1954.
Lehmer, D. H. and Lehmer, E.; and Shanks, D. "Integer Sequences Having Prescribed Quadratic Character." Math. Comput. 24, 433-451, 1970.
Lukes, R. F.; Patterson, C. D.; and Williams, H. C. "Some Results on Pseudosquares." Math. Comput. 65, 361-372 and S25-S27, 1996.
Schinzel, A. "On Pseudosquares." In New Trends in Probability and Statistics, Vol. 4: Analytic and Probabilistic Methods in Number Theory (Ed. A. Laurinčikas, E. Manstavičius, and V. Stakenas). Utrecht, Netherlands: VSP, pp. 213-220, 1997.
Sloane, N. J. A. Sequence A002189/M5039 in "The On-Line Encyclopedia of Integer Sequences."
Stephens, A. J. and Williams, H. C. "An Open Architecture Number Sieve." It Number Theory and Cryptography (Sydney, 1989). Cambridge, England: Cambridge University Press, pp. 38-75, 1990.
Williams, H. C. and Shallit, J. O. "Factoring Integers Before Computers." In Mathematics of Computation 1943-1993 (Vancouver, 1993) (Ed. W. Gautschi). Providence, RI: Amer. Math. Soc., pp. 481-531, 1994.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|