The angle of aberration
 

Bradley remembered this work of Roemer, neglected for half a century. He also knew that the velocity of the Earth in its heliocentric orbit was about 30 km s⁻¹ in a direction always at right angles to it radius vector (assuming the Earth’s orbit to be circular). He now had all the information required to explain the phenomena he had observed and produce a formula to predict them.
In everyday life we are familiar with a number of examples embodying the principle involved. For instance, in a stationary car on a rainy day we see the raindrops stream downwards. But when the car moves, the raindrops’ paths slant so that they appear to be coming from a direction between directly overhead and the direction in which the car is travelling.

Figure 1. The effect of aberration.

In figure 1, let light from a star X enter a telescope at A so that the observer sees the star in the middle of the field of view. The telescope, because of the Earth’s orbital velocity v km s⁻¹, is moving in the direction EE₁. By the time the light travelling with velocity c km s⁻¹ (c = 299 792·5 km s⁻¹) has reached the foot of the telescope, the telescope has moved into the position E1B. To the observer, the star appears to lie in the direction E1B because the telescope has had to be tilted slightly away from the true direction of the star towards the instantaneous direction in which the observer is moving.
The angle of aberration, Δθ, is obtained by considering ΔAEE₁ in which the distances EE₁ and AE₁ are proportional to v and c respectively. If we take ∠AE₁D = θ and ∠AED = θ₁, then

Figure 2. The aberrational ellipse.

or

Hence,

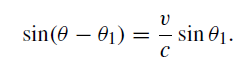
Remembering that θ − θ₁ = Δθ is a small angle (the quantity v/c ∼ 1/10 000), and expressing Δθ in seconds of arc, we may write

or
Δθ = κ sin θ. (1)
The constant κ is called the constant of aberration; its value is 20''·496. The angle of aberration
Δθ obviously depends upon the value of θ, the angle between the star’s direction and the instantaneous direction in which the observing is travelling. This is the direction D in which the Earth is moving, a direction known as the apex of the Earth’s way (figure 2) and which has a longitude always 90^◦ less than that of the Sun (DS). The Sun possessed that longitude three months previously, which Bradley realized was the explanation why his observations were always three months out of step with the ones he expected. Just as in the case of stellar parallax, the star appears to move in an ellipse about its heliocentric position X and just as in the case of parallax, it may easily be shown that the major axis of this ellipse, of value 40''·992, is parallel to the ecliptic. The shape of this aberrational ellipse obviously depends upon the star’s position on the celestial sphere. For a star on the ecliptic, the ellipse degenerates into an arc of length 2κ and for a star at the pole of the ecliptic, the ellipse is a circle.

اخر الاخبار

اخبار العتبة العباسية المقدسة

قسم الإعلام يشارك في الاجتماع التحضيري لمناقشة الخطة الإعلامية لزيارة عاشوراء

بحضور متوليها الشرعي.. العتبة العباسية المقدسة تواصل إقامة المجالس الحسينية لإحياء شهر المحرم

قسم الشؤون الفكرية يطلق برنامجه التبليغي في أكثر من 20 دولة إفريقية

شعبتا الخطابة النسوية والتوجيه الديني تواصلان إقامة المجالس الحسينية في مرقد أبي الفضل العباس (عليه السلام)

المزيد

الآخبار الصحية

دراسة تكشف علاقة خطيرة بين عمر الأم وصحة مولودها

دراسة تحذر.. اضطراب نوم بسيط قد يسبب الموت المبكر ؟

الاستحمام بالماء الساخن.. راحة مؤقتة وأضرار دائمة للبشرة

ماذا يحدث للجسم عند تخطي وجبة الإفطار؟

المزيد

الآخبار التكنلوجية

كيف تساعد الصيانة الوقائية في الحفاظ على كفاءة التكييف في سيارتك ؟

في ظاهرة غريبة حيرت العلماء.. كوكبنا قد يسجل أقصر يوم في التاريخ هذا الصيف!

السد الصيني العملاق يعيق دوران الأرض ويغيّر شكلها ؟

السعودية تطلق 10 تجارب علمية إلى محطة الفضاء الدولية

المزيد

مواضيع ذات صلة

اختبار الانفجار الهائل

الكوسمولوجيا وأشكال كالابي - ياو

التخمينات الكوسمولوجيا والنظرية النهائية

اختبار الانفجار الهائل

النموذج القياسي للكوسمولوجيا، أو علم الكون

تأملات في علم الكون

المذنبات

الصعود إلى الفضاء

اختلاف الليل والنهار

تصنيع الصاروخ و اطلاقة

الكويكبات والمذنبات

صورة الحجر الأزتكي (فهم وإدراك الحضارة الآزيتية )