Ferguson-Forcade Algorithm

The first practical algorithm for determining if there exist integers 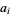 for given real numbers  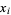such that

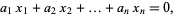or else establish bounds within which no such integer relation can exist (Ferguson and Forcade 1979). The algorithm therefore became the first viable generalization of the Euclidean algorithm to 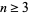 variables.

A nonrecursive variant of the original algorithm was subsequently devised by Ferguson (1987). The Ferguson-Forcade algorithm has been shown to be polynomial time in the logarithm in the size of a smallest relation, but has not been shown to be polynomial in dimension (Ferguson et al. 1999).

REFERENCES:

Bailey, D. H. "Numerical Results on the Transcendence of Constants Involving 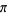, , 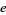and Euler's Constant." Math. Comput. 50, 275-281, 1988.

Bergman, G. "Notes on Ferguson and Forcade's Generalized Euclidean Algorithm." Unpublished notes. Berkeley, CA: University of California at Berkeley, Nov. 1980.

Ferguson, H. R. P. "A Short Proof of the Existence of Vector Euclidean Algorithms." Proc. Amer. Math. Soc. 97, 8-10, 1986.

Ferguson, H. R. P. "A Non-Inductive GL(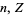) Algorithm that Constructs Linear Relations for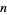 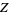 -Linearly Dependent Real Numbers." J. Algorithms 8, 131-145, 1987.

Ferguson, H. R. P.; Bailey, D. H.; and Arno, S. "Analysis of PSLQ, An Integer Relation Finding Algorithm." Math. Comput. 68, 351-369, 1999.

Ferguson, H. R. P. and Forcade, R. W. "Generalization of the Euclidean Algorithm for Real Numbers to All Dimensions Higher than Two." Bull. Amer. Math. Soc. 1, 912-914, 1979.

Ferguson, H. R. P. and Forcade, R. W. "Multidimensional Euclidean Algorithms." J. reine angew. Math. 334, 171-181, 1982.

Gibbs, W. W. "A Digital Slice of Pi. The New Way to do Pure Math: Experimentally." Sci. Amer. 288, 23-24, May 2003.