Gauss's Cyclotomic Formula

Let 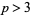 be a prime number, then

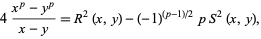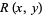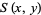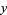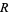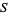where  and  are homogeneous polynomials in  and  with integer coefficients. Gauss (1965, p. 467) gives the coefficients of  and  up to .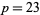

Kraitchik (1924) generalized Gauss's formula to odd squarefree integers 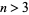. Then Gauss's formula can be written in the slightly simpler form

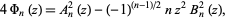where 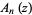 and 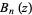 have integer coefficients and are of degree  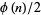and 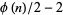, respectively, with  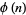the totient function and  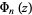a cyclotomic polynomial. In addition,  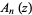is symmetric if  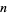is even; otherwise it is antisymmetric.  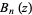is symmetric in most cases, but it antisymmetric if  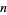is of the form  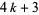(Riesel 1994, p. 436). The following table gives the first few  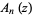and 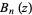s (Riesel 1994, pp. 436-442).

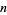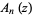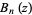5		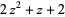1
7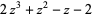
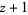11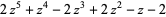

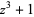REFERENCES:

Gauss, C. F. §356-357 in Untersuchungen über höhere Arithmetik. New York: Chelsea, pp. 425-428 and 467, 1965.

Kraitchik, M. Recherches sue la théorie des nombres, tome I. Paris: Gauthier-Villars, pp. 93-129, 1924.

Kraitchik, M. Recherches sue la théorie des nombres, tome II. Paris: Gauthier-Villars, pp. 1-5, 1929.

Riesel, H. "Gauss's Formula for Cyclotomic Polynomials." In tables at end of Prime Numbers and Computer Methods for Factorization, 2nd ed. Boston, MA: Birkhäuser, pp. 436-442, 1994.