المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Linnik,s Theorem |
 557
 03:23 مساءً
date: 17-3-2020 |
Author : Linnik, U. V. 
Book or Source : "On the Least Prime in an Arithmetic Progression. I. The Basic Theorem." Mat. Sbornik N. S 
Page and Part : ...|
Read More
Date: 22-7-2020
855
Date: 24-12-2020
628
Date: 22-10-2020
556
|
Let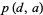 
be the smallest prime in the arithmetic progression 
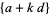for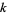 
an integer 
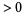. Let
 |
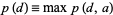such that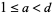 
and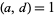 
. Then there exists a 
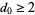and an 
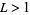such that 
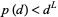for all 
. 
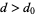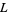is known as Linnik's constant.
REFERENCES:
Finch, S. R. "Linnik's Constant." §2.12 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 127-130, 2003.
Linnik, U. V. "On the Least Prime in an Arithmetic Progression. I. The Basic Theorem." Mat. Sbornik N. S. 15 (57), 139-178, 1944.
Linnik, U. V. "On the Least Prime in an Arithmetic Progression. II. The Deuring-Heilbronn Phenomenon" Mat. Sbornik N. S. 15 (57), 347-368, 1944.
|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|
