Hafner-Sarnak-McCurley Constant

Given two randomly chosen 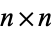 integer matrices, what is the probability  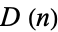that the corresponding determinants are relatively prime? Hafner et al. (1993) showed that

(1)

where 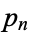 is the 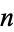th prime.

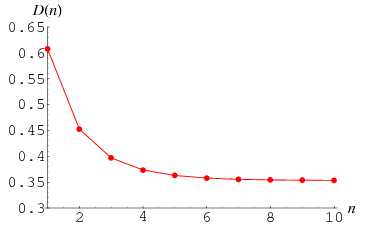
The case 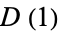 is just the probability that two random integers are relatively prime,

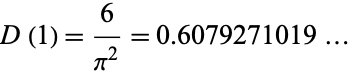(2)

(OEIS A059956). No analytic results are known for 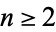. Approximate values for the first few  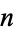are given by

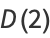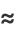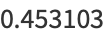			(3)
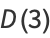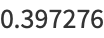			(4)
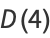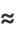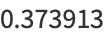			(5)
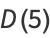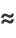			(6)

Vardi (1991) computed the limit

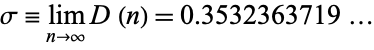(7)

(A085849). The speed of convergence is roughly 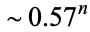 (Flajolet and Vardi 1996).

REFERENCES:

Finch, S. R. "Hafner-Sarnak-McCurley Constant." §2.5 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 110-112, 2003.

Flajolet, P. and Vardi, I. "Zeta Function Expansions of Classical Constants." Unpublished manuscript. 1996. http://algo.inria.fr/flajolet/Publications/landau.ps.

Hafner, J. L.; Sarnak, P.; and McCurley, K. "Relatively Prime Values of Polynomials." In A Tribute to Emil Grosswald: Number Theory and Related Analysis (Ed. M. Knopp and M. Seingorn). Providence, RI: Amer. Math. Soc., 1993.

Sloane, N. J. A. Sequences A059956 and A085849 in "The On-Line Encyclopedia of Integer Sequences."

Vardi, I. Computational Recreations in Mathematica. Redwood City, CA: Addison-Wesley, 1991.