


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 23-12-2019
Date: 24-2-2020
Date: 12-3-2020
|
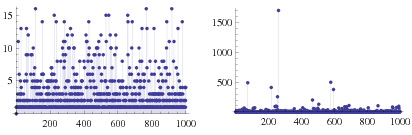
The simple continued fraction of the Golomb-Dickman constant 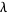 is [0; 1, 1, 1, 1, 1, 22, 1, 2, 3, 1, 1, 11, ...] (OEIS A225336). Note that this continued fraction appears to contain an unusually large number of 1s (and in general small terms), with 41.6% of the first 14510 terms being 1, 16.8% being 2, and so on (E. Weisstein, Jul. 25, 2013).
is [0; 1, 1, 1, 1, 1, 22, 1, 2, 3, 1, 1, 11, ...] (OEIS A225336). Note that this continued fraction appears to contain an unusually large number of 1s (and in general small terms), with 41.6% of the first 14510 terms being 1, 16.8% being 2, and so on (E. Weisstein, Jul. 25, 2013).
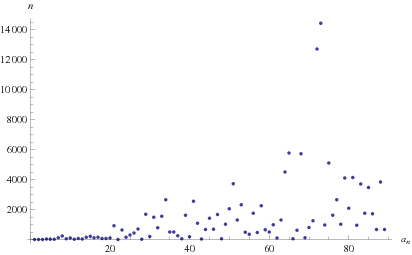
The plot above shows the positions of the first occurrences of 1, 2, 3, ... in the continued fraction, the first few of which are 1, 8, 9, 30, 25, 18, 110, 242, 59, 100, 12, 71, 28, 153, 225, 114, 159, 66, ... (OEIS A225364). The smallest positive integers not appearing in the first 14510 terms of the continued fraction are 90, 108, 110, 124, ... (E. W. Weisstein, Jul. 25, 2013).
The sequence of largest terms in the continued fraction is 0, 1, 22, 28, 43, 48, 66, 491, 1706, 4763, 38371, ... (OEIS A225337), which occur at positions 0, 1, 6, 24, 39, 50, 52, 72, 259, 1002, 4610, ... (OEIS A225363).
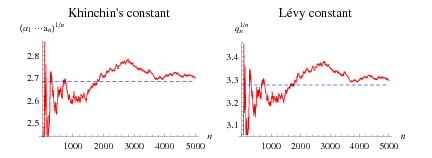
Let the continued fraction of 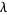 be denoted
be denoted ![[a_0;a_1,a_2,...]](http://mathworld.wolfram.com/images/equations/Golomb-DickmanConstantContinuedFraction/Inline3.gif) and let the denominators of the convergents be denoted
and let the denominators of the convergents be denoted 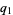 ,
, 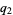 , ...,
, ..., 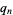 . Then plots above show successive values of
. Then plots above show successive values of 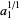 ,
, 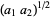 ,
, 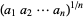 , which appear to converge to Khinchin's constant (left figure) and
, which appear to converge to Khinchin's constant (left figure) and 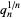 , which appear to converge to the Lévy constant (right figure), although neither of these limits has been rigorously established.
, which appear to converge to the Lévy constant (right figure), although neither of these limits has been rigorously established.
REFERENCES:
Sloane, N. J. A. Sequences A225336, A225337, A225363, and A225364 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
للحفاظ على صحة العين.. تناول هذا النوع من المكسرات
|
|
|
|
|
|
|
COP29.. رئيس الإمارات يؤكد أهمية تسريع العمل المناخي
|
|
|
|
|
|
|
المجمع العلمي يختتم دورته التطويرية الثانية للمؤسسات القرآنية
|
|
|