


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 3-3-2020
Date: 24-7-2020
Date: 8-7-2020
|
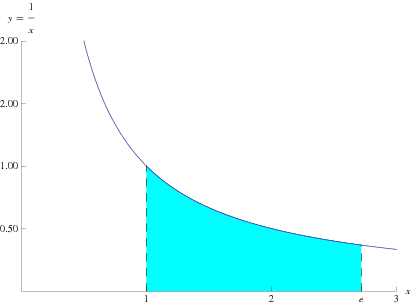
The constant 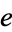 is base of the natural logarithm.
is base of the natural logarithm. 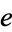 is sometimes known as Napier's constant, although its symbol (
is sometimes known as Napier's constant, although its symbol (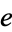 ) honors Euler.
) honors Euler.
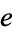 is the unique number with the property that the area of the region bounded by the hyperbola
is the unique number with the property that the area of the region bounded by the hyperbola 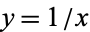 , the x-axis, and the vertical lines
, the x-axis, and the vertical lines 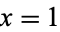 and
and 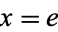 is 1. In other words,
is 1. In other words,
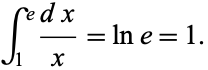 |
(1) |
With the possible exception of 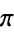 ,
, 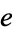 is the most important constant in mathematics since it appears in myriad mathematical contexts involving limits and derivatives. The numerical value of
is the most important constant in mathematics since it appears in myriad mathematical contexts involving limits and derivatives. The numerical value of 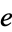 is
is
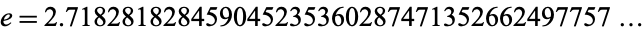 |
(2) |
(OEIS A001113).
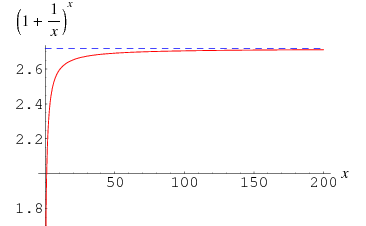
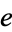 can be defined by the limit
can be defined by the limit
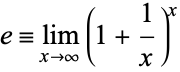 |
(3) |
(illustrated above), or by the infinite series
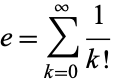 |
(4) |
as first published by Newton (1669; reprinted in Whiteside 1968, p. 225).
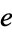 is given by the unusual limit
is given by the unusual limit
![lim_(n->infty)[((n+1)^(n+1))/(n^n)-(n^n)/((n-1)^(n-1))]=e](http://mathworld.wolfram.com/images/equations/e/NumberedEquation5.gif) |
(5) |
(Brothers and Knox 1998).
Euler (1737; Sandifer 2006) proved that 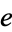 is irrational by proving that
is irrational by proving that 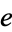 has an infinite simple continued fraction (
has an infinite simple continued fraction (![e=[2,1,2,1,1,4,1,1,6,...]](http://mathworld.wolfram.com/images/equations/e/Inline15.gif) ; Nagell 1951), and Liouville proved in 1844 that
; Nagell 1951), and Liouville proved in 1844 that 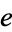 does not satisfy any quadratic equation with integral coefficients (i.e., if it is algebraic, it must be algebraic of degree greater than 2). Hermite subsequently settled the issue, proving
does not satisfy any quadratic equation with integral coefficients (i.e., if it is algebraic, it must be algebraic of degree greater than 2). Hermite subsequently settled the issue, proving 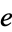 to be transcendental in 1873. However,
to be transcendental in 1873. However, 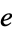 is the "least" transcendental possible, with irrationality measure
is the "least" transcendental possible, with irrationality measure 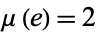 .
.
Sondow (2006) proved that 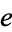 is irrational using a construction for
is irrational using a construction for 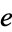 as the intersection of a nested sequence of closed intervals. This method also provides a measure of irrationality in terms of the Smarandache function (denoted here as
as the intersection of a nested sequence of closed intervals. This method also provides a measure of irrationality in terms of the Smarandache function (denoted here as 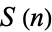 instead of the conventional
instead of the conventional 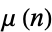 in order to avoid confusion with the irrationality measure) by showing that if
in order to avoid confusion with the irrationality measure) by showing that if 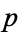 and
and 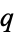 are any integers with
are any integers with 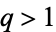 , then
, then
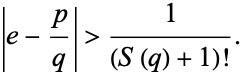 |
(6) |
It is not known if 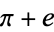 or
or 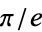 is irrational. It is known that
is irrational. It is known that 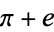 and
and 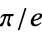 do not satisfy any polynomial equation of degree
do not satisfy any polynomial equation of degree 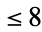 with integer coefficients of average size
with integer coefficients of average size 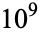 (Bailey 1988, Borwein et al. 1989), but it is not known if either of these is transcendental.
(Bailey 1988, Borwein et al. 1989), but it is not known if either of these is transcendental.
It is not known if 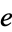 is normal to any base (Stoneham 1970).
is normal to any base (Stoneham 1970).
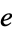 has the series representation
has the series representation
![e=[sum_(k=0)^infty((-1)^k)/(k!)]^(-1),](http://mathworld.wolfram.com/images/equations/e/NumberedEquation7.gif) |
(7) |
as well as
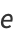 |
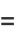 |
![[sum_(k=0)^(infty)(1-2k)/((2k)!)]^(-1)](http://mathworld.wolfram.com/images/equations/e/Inline37.gif) |
(8) |
 |
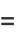 |
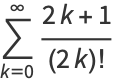 |
(9) |
 |
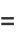 |
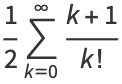 |
(10) |
 |
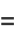 |
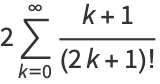 |
(11) |
 |
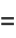 |
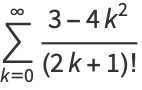 |
(12) |
 |
 |
 |
(13) |
 |
 |
![[sum_(k=0)^(infty)(4k+3)/(2^(2k+1)(2k+1)!)]^2.](http://mathworld.wolfram.com/images/equations/e/Inline55.gif) |
(14) |
The special case of the Euler formula
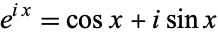 |
(15) |
with 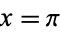 gives the beautiful identity
gives the beautiful identity
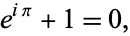 |
(16) |
an equation connecting the fundamental numbers i, pi, 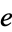 , 1, and 0 (zero) and involving the fundamental operations of equality (
, 1, and 0 (zero) and involving the fundamental operations of equality (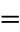 ), addition (
), addition (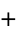 ), multiplication (
), multiplication (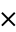 ), and exponentiation.
), and exponentiation.
A nested series for 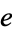 can be obtained by rewriting the series (2) for
can be obtained by rewriting the series (2) for 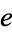 as
as
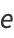 |
 |
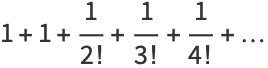 |
(17) |
 |
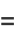 |
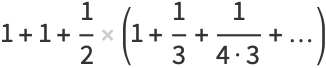 |
(18) |
 |
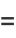 |
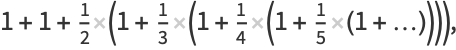 |
(19) |
which gives a pretty nested radical result when 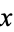 is taken to the power of both sides.
is taken to the power of both sides.
An unexpected Wallis-like formula for 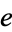 is given by the Pippenger product
is given by the Pippenger product
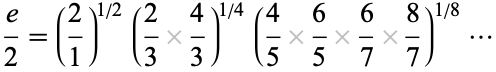 |
(20) |
(OEIS A084148 and A084149; Pippenger 1980). Another product for 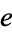 given by
given by
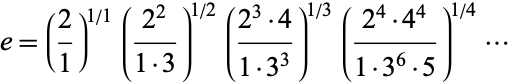 |
(21) |
due to Guillera (Sondow 2006). This is analogous to the products
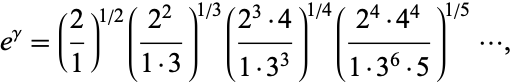 |
(22) |
and
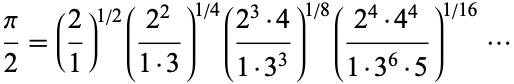 |
(23) |
(Guillera and Sondow 2005, Sondow 2006).
Using the recurrence relation
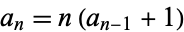 |
(24) |
with 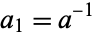 , compute
, compute
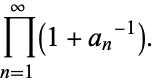 |
(25) |
The result is 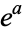 . Gosper gives the unusual equation connecting
. Gosper gives the unusual equation connecting 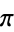 and
and 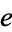 ,
,
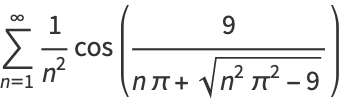 |
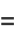 |
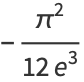 |
(26) |
 |
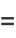 |
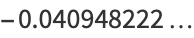 |
(27) |
(OEIS A100074).
Rabinowitz and Wagon (1995) give an algorithm for computing digits of 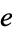 based on earlier digits (Borwein and Bailey 2003, p. 140), but a much simpler spigot algorithm was found by Sales in 1968. Around 1966, MIT hacker Eric Jensen wrote a very concise program (requiring less than a page of assembly language) that computed
based on earlier digits (Borwein and Bailey 2003, p. 140), but a much simpler spigot algorithm was found by Sales in 1968. Around 1966, MIT hacker Eric Jensen wrote a very concise program (requiring less than a page of assembly language) that computed 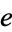 by converting from factorial base to decimal.
by converting from factorial base to decimal.
Let 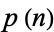 be the probability that a random one-to-one function on the integers 1, ...,
be the probability that a random one-to-one function on the integers 1, ..., 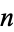 has at least one fixed point. Then
has at least one fixed point. Then
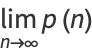 |
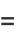 |
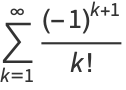 |
(28) |
 |
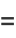 |
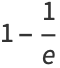 |
(29) |
 |
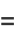 |
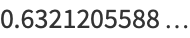 |
(30) |
(OEIS A068996).
Stirling's approximation gives
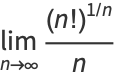 |
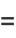 |
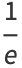 |
(31) |
 |
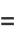 |
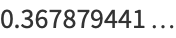 |
(32) |
(OEIS A068985).
Steiner's problem asks for the largest value of the function 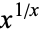 , which is given by
, which is given by 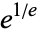 .
.
Examples of 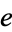 mnemonics (Gardner 1959, 1991) include:
mnemonics (Gardner 1959, 1991) include:
"By omnibus I traveled to Brooklyn" (6 digits).
"To disrupt a playroom is commonly a practice of children" (10 digits).
"It enables a numskull to memorize a quantity of numerals" (10 digits).
"I'm forming a mnemonic to remember a function in analysis" (10 digits).
"He repeats: I shouldn't be tippling, I shouldn't be toppling here!" (11 digits).
"In showing a painting to probably a critical or venomous lady, anger dominates. O take guard, or she raves and shouts" (21 digits). Here, the word "O" stands for the number 0.
A much more extensive mnemonic giving 40 digits is
"We present a mnemonic to memorize a constant so exciting that Euler exclaimed: '!' when first it was found, yes, loudly '!'. My students perhaps will compute 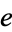 , use power or Taylor series, an easy summation formula, obvious, clear, elegant!"
, use power or Taylor series, an easy summation formula, obvious, clear, elegant!"
(Barel 1995). In the latter, 0s are represented with "!". A list of 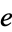 mnemonics in several languages is maintained by A. P. Hatzipolakis.
mnemonics in several languages is maintained by A. P. Hatzipolakis.
REFERENCES:
Bailey, D. H. "Numerical Results on the Transcendence of Constants Involving 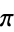 , e, and Euler's Constant." Math. Comput. 50, 275-281, 1988.
, e, and Euler's Constant." Math. Comput. 50, 275-281, 1988.
Barel, Z. "A Mnemonic for e." Math. Mag. 68, 253, 1995.
Baruvelle, H. V. "The Number e: The Base of Natural Logarithms." Math. Teacher 38, 350-355, 1945.
Borwein, J. and Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, 2003.
Borwein, J. M.; Borwein, P. B.; and Bailey, D. H. "Ramanujan, Modular Equations, and Approximations to Pi or How to Compute One Billion Digits of Pi." Amer. Math. Monthly 96, 201-219, 1989.
Brothers, H. J. "Improving the Convergence of Newton's Series Approximation for 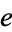 ." College Math. J. 35, 34-39, 2004.
." College Math. J. 35, 34-39, 2004.
Brothers, H. J. and Knox, J. A. "New Closed-Form Approximations to the Logarithmic Constant e." Math. Intell. 20, 25-29, 1998.
Caldwell, C. K. and Dubner, H. "Primes in Pi." J. Recr. Math. 29, 282-289, 1998.
Castellanos, D. "The Ubiquitous Pi. Part I." Math. Mag. 61, 67-98, 1988.
Conway, J. H. and Guy, R. K. The Book of Numbers. New York: Springer-Verlag, pp. 201 and 250-254, 1996.
Euler, L. "De fractionibus continuis dissertation." Comm. Acad. Sci. Petr. 9, 98-137, (1737) 1744. Reprinted in Leonhardi Euleri Opera Omnia, Ser. I, Vol. 14. Leipzig, Germany: Teubner, pp. 187-215, 1924.
Euler, L. "An Essay on Continued Fractions." Trans. M. F. Wyman and B. F. Wyman. Math. Systems Th. 18, 295-328, 1985.
Finch, S. R. "The Natural Logarithm Base." §1.3 in Mathematical Constants. Cambridge, England: Cambridge University Press, pp. 12-17, 2003.
Friedman, E. "Problem of the Month (August 2004)." http://www.stetson.edu/~efriedma/mathmagic/0804.html.
Gardner, M. "Memorizing Numbers." Ch. 11 in The Scientific American Book of Mathematical Puzzles and Diversions. New York: Simon and Schuster, pp. 103 and 109, 1959.
Gardner, M. "The Transcendental Number e." Ch. 3 in The Unexpected Hanging and Other Mathematical Diversions. Chicago, IL: Chicago University Press, pp. 34-42, 1991.
Gourdon, X. and Sebah, P. "The Constant e." http://numbers.computation.free.fr/Constants/E/e.html.
Guillera, J. and Sondow, J. "Double Integrals and Infinite Products for Some Classical Constants Via Analytic Continuations of Lerch's Transcendent." 16 June 2005. http://arxiv.org/abs/math.NT/0506319.
Hatzipolakis, A. P. "PiPhilology." http://www.cilea.it/~bottoni/www-cilea/F90/piphil.htm.
Hermite, C. "Sur la fonction exponentielle." C. R. Acad. Sci. Paris 77, 18-24, 74-79, and 226-233, 1873.
Knox, J. A. and Brothers, H. J. "Novel Series-Based Approximations to e." College Math. J. 30, 209-215, 1999.
Le Lionnais, F. Les nombres remarquables. Paris: Hermann, p. 47, 1983.
Maor, E. e: The Story of a Number. Princeton, NJ: Princeton University Press, 1994.
Minkus, J. "A Continued Fraction." Problem 10327. Amer. Math. Monthly 103, 605-606, 1996.
Mitchell, U. G. and Strain, M. "The Number e." Osiris 1, 476-496, 1936.
Nagell, T. "Irrationality of the numbers e and 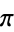 ." §13 in Introduction to Number Theory. New York: Wiley, pp. 38-40, 1951.
." §13 in Introduction to Number Theory. New York: Wiley, pp. 38-40, 1951.
Newton, I. The Mathematical Papers of Isaac Newton, Vol. 2.: 1667-1670 (Ed. D. T. Whiteside). New York: Cambridge University Press, 1968.
Pippenger, N. "An Infinite Product for 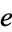 ." Amer. Math. Monthly 87, 391, 1980.
." Amer. Math. Monthly 87, 391, 1980.
Plouffe, S. "Table of Current Records for the Computation of Constants." http://pi.lacim.uqam.ca/eng/records_en.html.
Rabinowitz, S. and Wagon, S. "A Spigot Algorithm for the Digits of 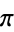 ." Amer. Math. Monthly 102, 195-203, 1995.
." Amer. Math. Monthly 102, 195-203, 1995.
Reid, C. In From Zero to Infinity, 4th ed. Washington, DC: Math. Assoc. Amer., 1992.
Sandifer, E. "How Euler Did It: Who proved 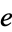 is Irrational?" Feb. 2006. http://www.maa.org/editorial/euler/How%20Euler%20Did%20It%2028%20e%20is%20irrational.pdf.
is Irrational?" Feb. 2006. http://www.maa.org/editorial/euler/How%20Euler%20Did%20It%2028%20e%20is%20irrational.pdf.
Sloane, N. J. A. Sequences A000029/M0563, A001113/M1727, A068985, A068996, A084148, A084149, and A100074 in "The On-Line Encyclopedia of Integer Sequences."
Sondow, J. "A Geometric Proof that 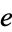 Is Irrational and a New Measure of Its Irrationality." Amer. Math. Monthly 113, 637-641, 2006.
Is Irrational and a New Measure of Its Irrationality." Amer. Math. Monthly 113, 637-641, 2006.
Stoneham, R. "A General Arithmetic Construction of Transcendental Non-Liouville Normal Numbers from Rational Functions." Acta Arith. 16, 239-253, 1970.
Wall, H. S. Analytic Theory of Continued Fractions. New York: Chelsea, 1948.
Weisstein, E. W. "Books about e." http://www.ericweisstein.com/encyclopedias/books/e.html.
Wells, D. The Penguin Dictionary of Curious and Interesting Numbers. Middlesex, England: Penguin Books, p. 46, 1986.



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|