
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 13-2-2020
Date: 8-9-2020
Date: 6-10-2020
|
The multiplicative suborder of a number 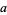 (mod
(mod 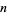 ) is the least exponent
) is the least exponent 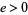 such that
such that 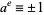 (mod
(mod 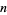 ), or zero if no such
), or zero if no such 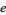 exists. An
exists. An 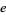 always exists if
always exists if 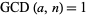 and
and 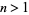 .
.
This function is denoted 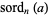 and can be implemented in the Wolfram Language as:
and can be implemented in the Wolfram Language as:
Suborder[a_,n_] := If[n>1&& GCD[a,n] == 1,
Min[MultiplicativeOrder[a, n, {-1, 1}]],
0
]
The following table summarizes 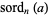 for small values of
for small values of 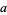 and
and 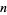 .
.
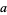 |
OEIS |  for for  , 1, ... , 1, ... |
| 2 | 0, 0, 0, 1, 0, 2, 0, 3, 0, 3, 0, 5, 0, 6, 0, ... | |
| 3 | A103489 | 0, 0, 1, 0, 1, 2, 0, 3, 2, 0, 2, 5, 0, 3, 3, ... |
| 4 | 0, 0, 0, 1, 0, 1, 0, 3, 0, 3, 0, 5, 0, 3, 0, ... | |
| 5 | A103491 | 0, 0, 1, 1, 1, 0, 1, 3, 2, 3, 0, 5, 2, 2, 3, ... |
REFERENCES:
Sloane, N. J. A. Sequences A103489 and A103491 in "The On-Line Encyclopedia of Integer Sequences."
Wolfram, S.; Martin, O.; and Odlyzko, A. M. "Algebraic Properties of Cellular Automata." Comm. Math. Phys. 93, 219-258, 1984.



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|